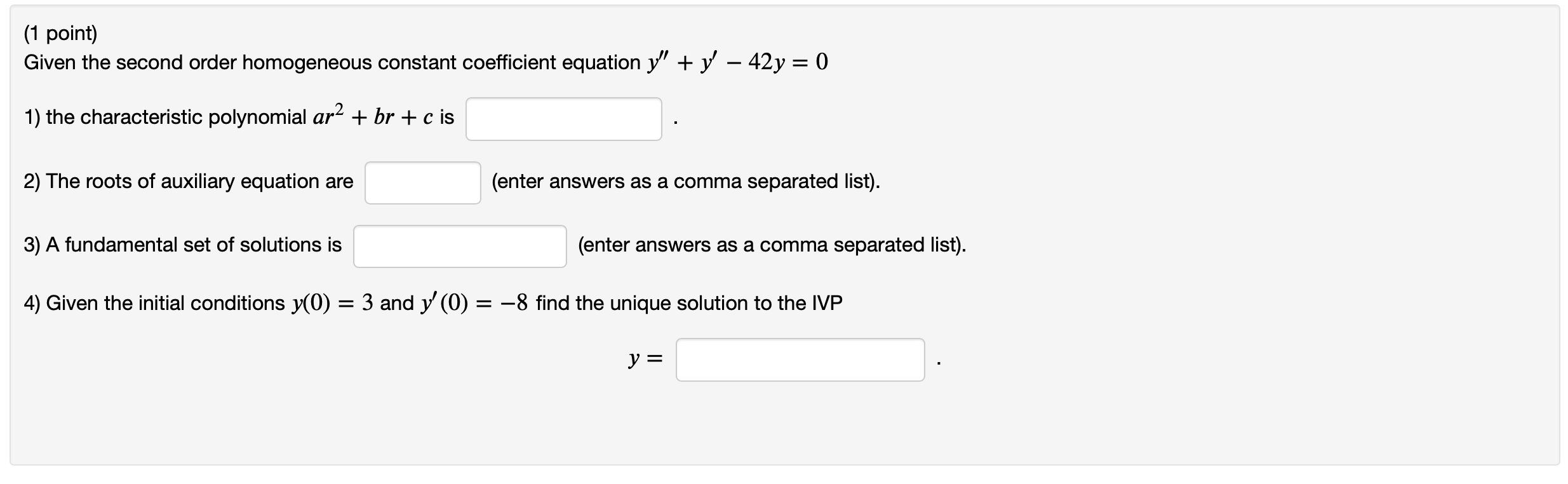
Question: Three questions below I need them solved pretty quickly thank you Entered Answer Preview Result Message (r^2)-10*r+25 r2 - 10r + 25 correct 5. 5
Three questions below I need them solved pretty quickly thank you


Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


