Time Complexity and Algorithms

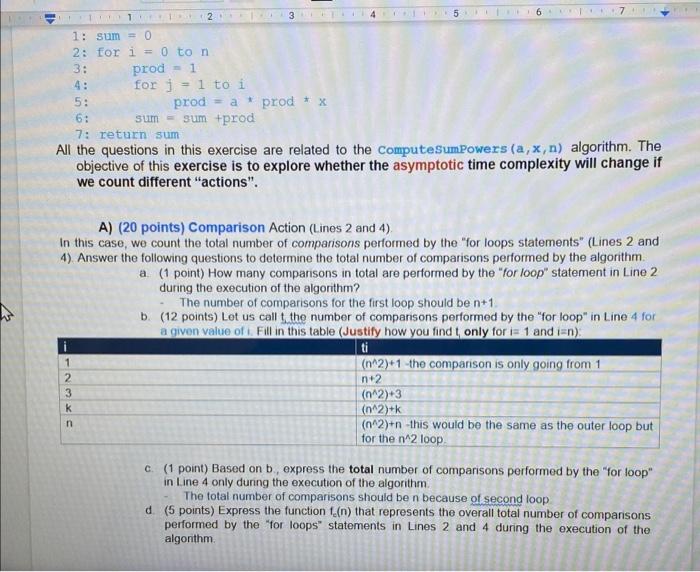
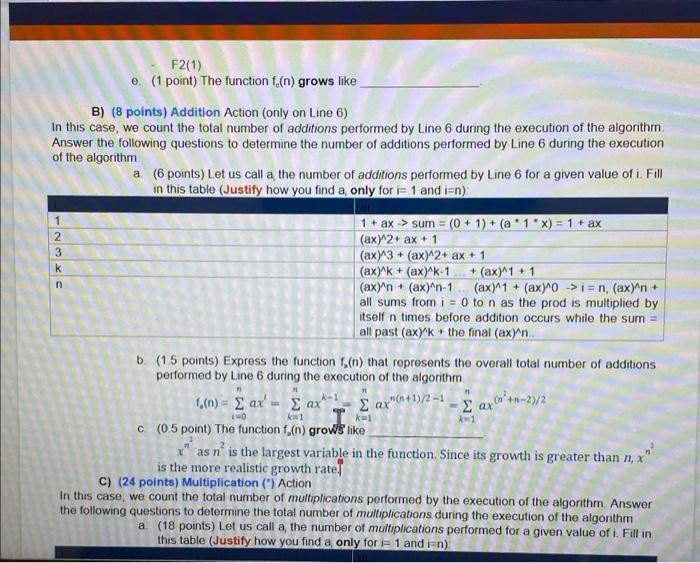
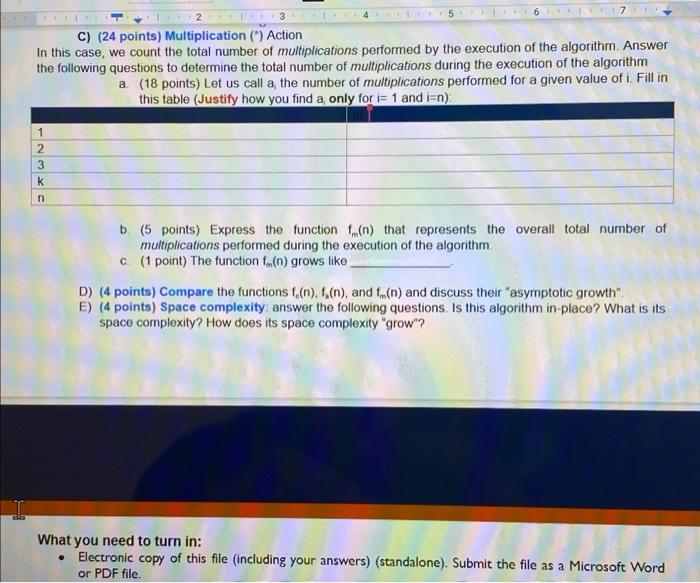
TIT 6 4 2 7 3 5 1: sum = 0 2: for i = 0 ton 3: prod = 1 4: for j = 1 to i 5: prod = a + prod ** 6: sum - sum +prod 7: return sum All the questions in this exercise are related to the computeSumPowers (a,x,n) algorithm. The objective of this exercise is to explore whether the asymptotic time complexity will change if we count different "actions". A) (20 points) Comparison Action (Lines 2 and 4). In this case, we count the total number of comparisons performed by the "for loops statements (Lines 2 and 4). Answer the following questions to determine the total number of comparisons performed by the algorithm a (1point) How many comparsons in total are performed by the "for loop" statement in Line 2 during the execution of the algorithm? The number of comparisons for the first loop should be n+1 b. (12 points) Let us call t the number of compansons performed by the "for loop" in Line 4 for a given value of t. Fill in this table (Justify how you find t only for i= 1 and ian) ti (n^2)+1 the comparison is only going from 1 n.2 (n^2)+3 (n^2)+k (n^2)+n this would be the same as the outer loop but for the n^2 loop 1 2 3 n c. (1 point) Based on b., express the total number of comparisons performed by the "for loop" in Line 4 only during the execution of the algorithm The total number of comparisons should be n because of second loop d. (5 points) Express the function 1.(n) that represents the overall total number of compansons performed by the "for loops" statements in Lines 2 and 4 during the execution of the algorithm F2(1) e. (1 point) The function f(n) grows like B) (8 points) Addition Action (only on Line 6) In this case, we count the total number of additions performed by Line 6 during the execution of the algorithm Answer the following questions to determine the number of additions performed by Line 6 during the execution of the algorithm a (6 points) Let us call a the number of additions performed by Line 6 for a given value of i. Fill in this table (Justify how you find a only for i= 1 and i=n) 1 -WN- 3 + 1 + ax -> sum = (0 + 1) + (a '1' x) = 1 + ax (ax)^2 + ax + 1 (ax)^3 + (ax)^2+ ax + 1 (ax) k + (ax)\k-1 + (ax) 1 + 1 (ax)^n + (ax)^n-1. (ax)^1 + (ax)^0 ->i= n, (ax)^n + all sums from i = 0 to n as the prod is multiplied by itself n times before addition occurs while the sum = all past (ax) k + the final (axn b. (1.5 points) Express the function (n) that represents the overall total number of additions performed by Line 6 during the execution of the algorithm 1,(n) = ax' = az x" (n +1)/2-1 c (0.5 point) The function f.(n) grows like x" as n is the largest variable in the function. Since its growth is greater than nex is the more realistic growth rate! C) (24 points) Multiplication (") Action In this case, we count the total number of multiplications performed by the execution of the algorithm Answer the following questions to determine the total number of multiplications during the execution of the algorithm a (18 points) Let us call a the number of multiplications performed for a given value of i. Fill in this table (Justify how you find a only for i= 1 and i=n) 1-1 2 axon*+--2)/2 kat ko 1 2. 51 C) (24 points) Multiplication (") Action In this case, we count the total number of multiplications performed by the execution of the algorithm Answer the following questions to determine the total number of multiplications during the execution of the algorithm a (18 points) Let us call a, the number of multiplications performed for a given value of i. Fill in this table (Justify how you find a only for i= 1 and i=n) PWN- b (5 points) Express the function (n) that represents the overall total number of multiplications performed during the execution of the algorithm c. (1 point) The function (n) grows like D) (4 points) Compare the functions fe(n). 1.(n), and (n) and discuss their "asymptotic growth". E) (4 points) Space complexity answer the following questions. Is this algorithm in-place? What is its space complexity? How does its space complexity "grow"? What you need to turn in: Electronic copy of this file (including your answers) (standalone). Submit the file as a Microsoft Word or PDF file