TITULAR, JOE I.                                                  August 8, 2023

PhD Math Ed Section 2

MATH ED 808 Advanced Topics in Geometry




Problem Set 2




Use the given below to answer items 1 and 2:

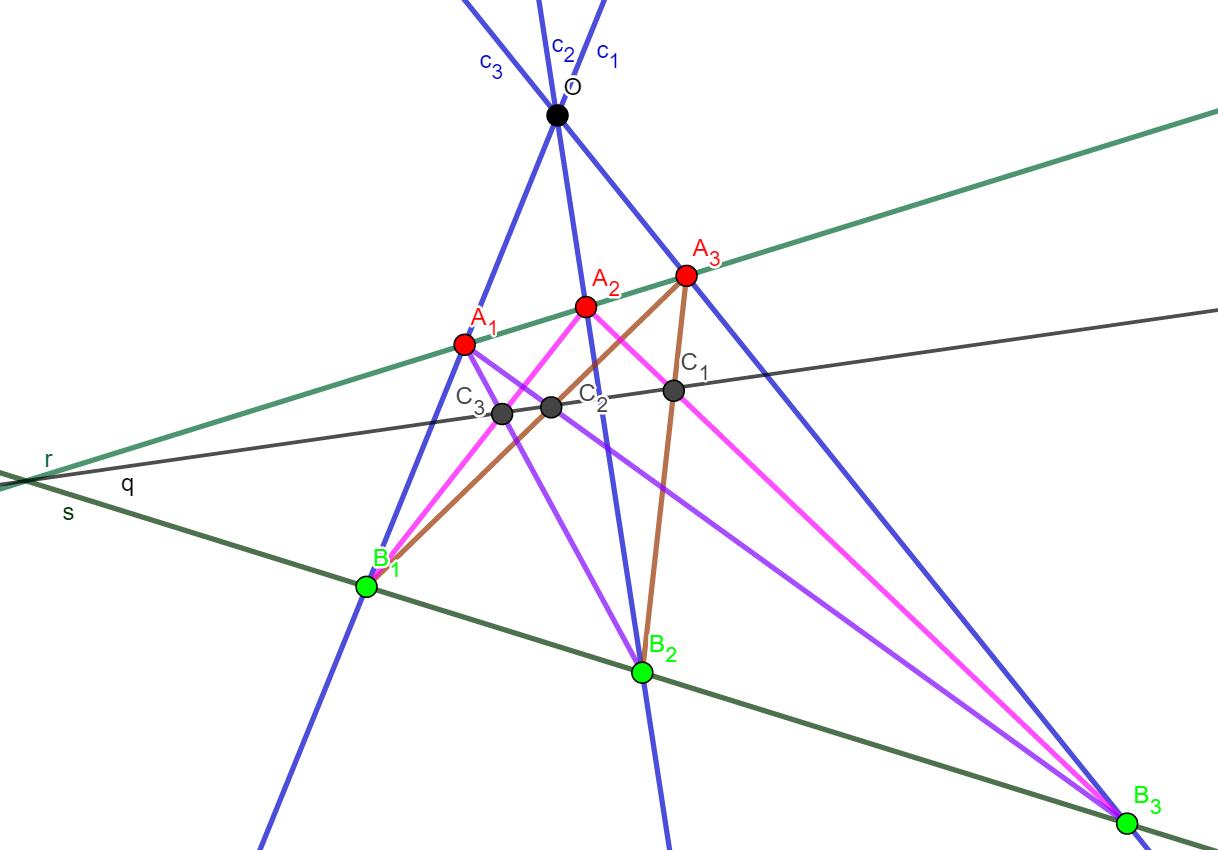
Given: In a projective plane, let A1, A2, A3 be distinct points on a line r and B1, B2, B3 be distinct points on another line s, and if c1 = A1 B1, c2 = A2 B2 and c3 = A3 B3 are on a point O, then the points, C1 = A3 B2 ·A2 B3, C2 = A3 B1 ·A1 B3 and C3 = A1 B2 ·A2 B1 are on line q that is concurrent with r and s.

1. Draw the figure corresponding to the given proposition.

Figure: 

1. State the duality of the given proposition.

Answer:

In a projective plane, let a1, a2, a3 be distinct lines on a point R and b1, b2, b3 be distinct lines on another point S, and if C1 = a1 b1, C2 = a2 b2 and C3 = a3 b3 are on a line o, then the lines,  c1 = a3 b2 ·a2 b3, c2 = a3 b1 ·a1 b3 and c3 = a1 b2 ·a2 b1 are on point Q that is collinear with R and S.

 

• In the figure below, show that there exists a projective transformation

R

Q

q

 

r(A1, B1, C1) -

 

 

^

 

s(A2, B2, C2) 

Solution: 

Use the given below to answer items 4 and 5:

Given 4 distinct points, W, X, Y, Z on a line a. To prove that there exists a projectivity which carries

W, X, Y, Z into X, W, Z, Y, consider the outline of the proof given below:

Proof: Project the points W, X, Y, Z from point A not on a. Section a by b (distinct from a and AY) on Y and obtain the points W’, X’, Y’, Z’, so that that Y = Y’. Join W’ and X meeting AZ = r at Z’’.

4.    Draw the figure with the conditions in the given and in the outline of the proof stated above.

• Supply the missing basis of each pencil and center of perspectivity that are established below.

 

 
  

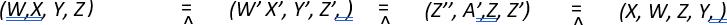• Use the figure drawn below to show that the pencil with elements B,A,D,E is projective to the pencil with elements Q, S, C, E.

 

 
 

03 b S BO B 2 B3