Topic: Discrete Mathematics and its Applications" Chapter 11: Tree: Tree Traversal,Spanning Trees, and Minimum Spanning Trees"

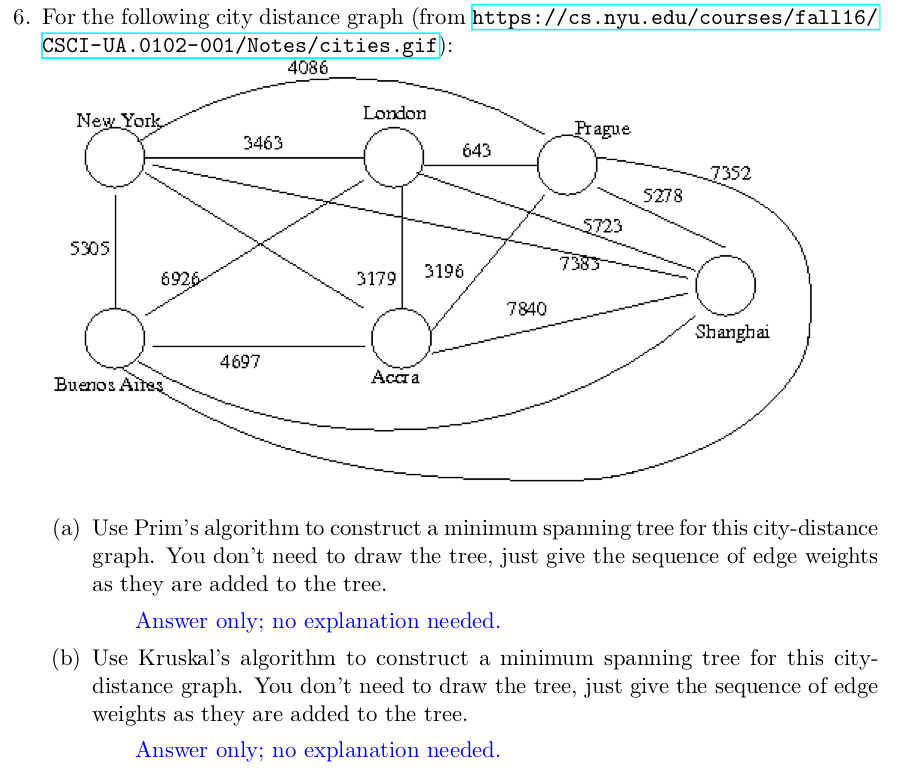
6. For the following city distance graph (from https://cs.nyu.edu/courses/fall16/ CSCI-UA.0102-001/Notes/cities.gif 4086 London New Yor Frague 3463 643 7352 5278 T23 5305 73 692 3179 3196 7840 Shanghai 4697 Accra Buenos Ai (a) Use Prim's algorithm to construct a minimum spanning tree for this city-distance graph. You don't need to draw the tree, just give the sequence of edge weights as they are added to the tree Answer only; no explanation needed (b) Use Kruskal's algorithm to construct a minimum spanning tree for this city- distance graph. You don't need to draw the tree, just give the sequence of edge weights as they are added to the tree. Answer only; no explanation needed