Question: tra Proplem & (Ceva's theorem). Let ABC, A' (BC), B' (AC) and C E (AB). Then the lines AA', BB' and CC' are concurrent

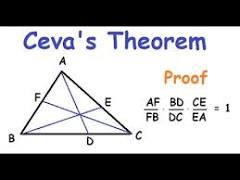
tra Proplem 8 (Ceva's theorem). Let ABC, A' (BC), B' (AC) and C B Ceva's Theorem A D E C Proof AF BD CE FB DC EA

tra Proplem & (Ceva's theorem). Let ABC, A' (BC), B' (AC) and C" E (AB). Then the lines AA', BB' and CC' are concurrent if and only if |BA| |CB'| |AC"| |A'C B'A |C'B| - 1. After establishing the above equivalence, conclude that the medians of every triangle are concurrent. B Ceva's Theorem A D E C Proof AF BD CE FB DC EA

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Cevas Theorem is a classical result in plane geometry that provides a necessary and sufficient condi... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Exactly 1 kg of a gas has a pressure of 9 8 . 0 0 kPa, a temperature of 1 7 . 0 0 o C and a volume of 1 . 1 0 m 3 . Determine its specific gas constant.

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

Given a byte-addressable memory with 256 bytes, suppose a memory dump yields the results shown below. The address of each memory cell is determined by its row and column. For example, memory address...

Please write code in C++ or C, details would be really helpful. If can, please give output screenshot. 1 Setting You already have recursive and stack-based code that prints all subsequences of an...

Jason uses the following steps to construct a perpendicular line through a point C on a line segment. Step 1: From point C, draw an arc intersecting the line segment in points A and B. Step 2: Using...

solve list language or list stretch you CANNOT use recursion to implement these functions. You MUST use a STACK BASED implementation. C OR C++ c language ing functions. Pay attention to the...

C++ (using recursion or stacks) List language(string input, int k). You will see a lot about lan- guages when you study Computational Models. Just think of the input string as a set of characters...

List language ( string input, int k ) . You will see a lot about languages when you study Computational Models. Just think of the input string 1 as a set of characters \ Sigma ( formally called an...

\fThecoordinatesoftheverticesofapolygonare(5, 1)(1, 3)(2, 3)(2, 2).and (3, 1). What is the perimeter of the polygon? Enter your answer as a decimal. rounded to the nearest tenth of a unit. in the...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Suppose that preferences are such that indifference curves are parallel shift along the identity line. That is, if x~ y then x+(a,...,a) ~ y+(a,...,a). Call these preferences parallel. Find a class...

Assume that there is an exogenous decline in the price of imported oil. Using the graphical analysis in this chapter, explain how such a shock would affect output and the price level. Explain the...

in the plane, the equation y = x ^ 2 defines a ( n ) in space, the equation y = x ^ 2 defines a ( n )

Consider the revised Coal Bank Hollow recycling problem discussed in section 5.5.4 of this chapter. We said that it is safest to assume the supply in a generalized network flow problem is capable of...

Contribution margin per unit approach for break-even and desired profit Information concerning a product produced by Hansen Company appears here: Sales price per unit...

The following data relating to direct materials cost for October of the current year are taken from the records of Good Clean Fun Inc., a manufacturer of organic toys: Quantity of direct materials...

With the growing popularity of casual surf print clothing, two recent MBA graduates decided to broaden this casual surf concept to encompass a surf lifestyle for the home. With limited capital, they...

Fanning Corporation incurs the following annual fixed costs: Item Cost Depreciation ...............$ 80,000 Officers' salaries............190,000 Long-term lease..............42,000 Property...

Grade 12 Calculus, Unit DerivativesAs part of their marketing class, some students decide to sell smoothies. During their test week, they sell 1500 smoothies at a price of $6.2 each. After doing some...

Please answer the following questions regarding the taxability of Social Security: a. A 68-year-old taxpayer has $20,000 in Social Security income and $100,000 in tax-free municipal bond income. Does...

Harold Conners (Social Security number 785-23-9873) lives at 13234 DeMilo Drive, Houston, TX 77052, and is self-employed for 2012. He estimates his required annual estimated tax payment for 2012 to...

In 2012, Gale and Cathy Alexander hosted an exchange student, Axel Muller, for 9 months. Axel was part of International Student Exchange Programs (a qualified organization). Axel attended tenth grade...

=+ (n1 1 n2 2 2 is the sum of the dfs contributed by the two samples). It can then be shown that the standardized variable t 5 (x1 2 x2) 2 (1 2 2) spA 1 n1 1 1 n2

=+Estimate for difference: 8.800 95% CI for difference: (6.498, 11.102) Calculate a two-sided 95% confidence interval for the difference in population means and confirm the lower and upper endpoints...

=+What is the confidence level for each of the following three confidence intervals for the mean of a normal population distribution? Which of the three intervals would you recommend be used, and...