Trees, Binary search trees in java:

This is my code, you can just edit the things you need or write new one. ```java

public static void main(String[] args) { Bst bst = new Bst(); //Todo Insertion Here, I couldnt do it // Traversal of bst System.out.print("Inorder Traversal:"); bst.inorder(); System.out.print(" Preorder Traversal:"); bst.preorder(); System.out.print(" Postorder Traversal:"); bst.postorder(); } } class Node{ int data; Node left; Node right; public Node(int data){ this.data=data; left = null; right = null; } public String toString(){ return data+" "; } }

class Bst { Node root; public Bst() { root = null; }

public void insert(int x) { Node n = new Node(x); if (root == null) { root = n; return; } Node current = root; while (current != null) { if (x

private void insertR(Node start, int x) { if (start == null) { start = new Node(x); return; } if (x

public void insertRec(int x){ insertR(root,x); } private int minimum(Node root){ int min = root.data; while (root.left != null){ min = root.left.data; root = root.left; } return min; }

private Node delete_Recursive(Node root, int key){ if (root == null) return root; if (key root.data) //traverse right subtree root.right = delete_Recursive(root.right, key); else{ // node contains only one child if (root.left == null) return root.right; else if (root.right == null) return root.left; root.data = minimum(root.right); root.right = delete_Recursive(root.right, root.data); } return root; } void delete(int key) { root = delete_Recursive(root, key); } //Traversal Methods public void inorder(){ inOrderRec(root); } private void inOrderRec(Node root){ if(root != null){ inOrderRec(root.left); System.out.print(root + " "); inOrderRec(root.right); } }

public void preorder(){ preOrderRec(root); } private void preOrderRec(Node root){ if(root != null){ System.out.print(root + " "); preOrderRec(root.left); preOrderRec(root.right); } }

public void postorder(){ postOrderRec(root); } private void postOrderRec(Node root){ if(root != null){ postOrderRec(root.left); postOrderRec(root.right); System.out.print(root + " "); } } }

```

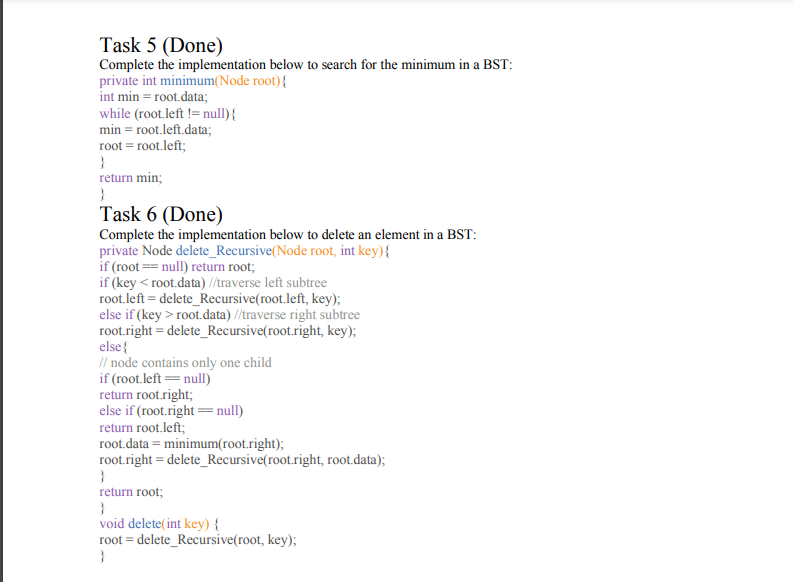
Task 1 We define the following class Node class Node \{ int data; Node left; Node right; public Node(int data)\{ this.data = data; left = null; right = null; \} public String toString O{ return data +" "; \} Task 2 Define the class BST public class Bst \{ Node root; public Bst ()\{ root = null; \} Task 3 Complete the iterative implementation below to insert a key in a BST: public void insert(int x){ Node n= new Node(x) \} Task 4 Complete the recursive implementation below to insert a key in a BST: private void insertR(Node start, int x){ \} public void insertRec(int x){ insertR(root,x); \} Task 5 (Done) Complete the implementation below to search for the minimum in a BST: private int minimum(Node root) \{ int min= root.data; while (root.left != null) \{ min= root.left.data; root = root.left; \} return min; \} Task 6 (Done) Complete the implementation below to delete an element in a BST: private Node delete_Recursive(Node root, int key)\{ if (root == null) return root; if (key root.data) //traverse right subtree root.right = delete_Recursive(root.right, key); else \{ // node contains only one child if ( root.left = = null) return root.right; else if (root.right = null) return root.left; root.data = minimum(root.right); root.right = delete_Recursive(root.right, root.data); \} return root; \} void delete(int key) \{ root = delete_Recursive(root, key); \} Task 7 Create the following Tree on slide 26 using the methods implemented in Lab 6. Task 8 Implement the methods inorder, preorder and postorder seen in the lecture. Task 9 Apply the methods implemented in Task 8 to the Tree and verify that you obtain the following results : Preorder Traversal: 3,13,22,19,26,54,71,33,14,11,87,8,56,9,75,28,15,10,63,36,7,69, 59,68,44 Inorder Traversal: 54,26,71,19,22,11,14,33,8,87,56,13,9,75,3,63,10,15,28,59,69,68, 7,36,44 Postorder Traversal: 54,71,26,19,11,14,8,56,87,33,22,75,9,13,63,10,15,59,68,69,7,44, 36 283