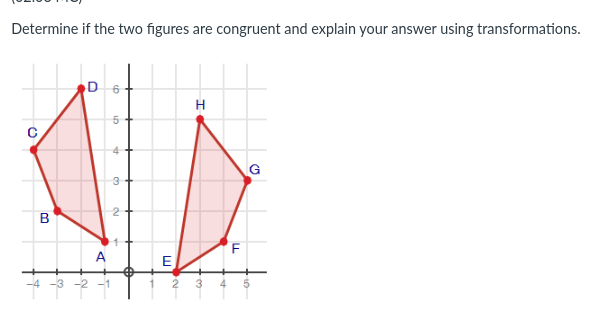
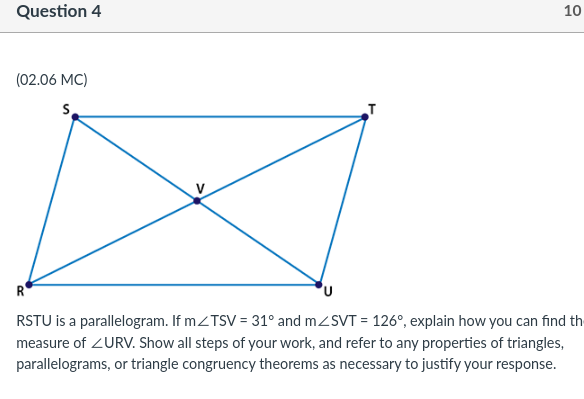
Triangle ABC has vertices A(-3, 1), B(-3, 4), and C(-7, 1). A. If AABC is translated according to the rule (x, y) - (x + 4, y - 3) to form AA'B'C', how is the translation described with words? (3 points) B. Where are the vertices of AA'B'C' located? Show your work or explain your steps. (4 points) C. Triangle A'B'C' is rotated 90" counterclockwise about the origin to form AA"B"C". Is AABC congruent to AA"B"C"? Give details to support your answer. (3 points)Determine if the two figures are congruent and explain your answer using transformations. D 6 H 5+ C 4 G 3 B 2 F A E 4 -3 -2 2 3 4In triangles ABC and LMN, ZA = ZL, ZB = ZM, and ZC = ZN. Is this information sufficient to prove triangles ABC and LMN congruent through ASA? Explain your answer.Question 4 10 (02.06 MC) S V R RSTU is a parallelogram. If m_TSV = 310 and m_SVT = 126, explain how you can find th measure of ZURV. Show all steps of your work, and refer to any properties of triangles, parallelograms, or triangle congruence theorems as necessary to justify your response