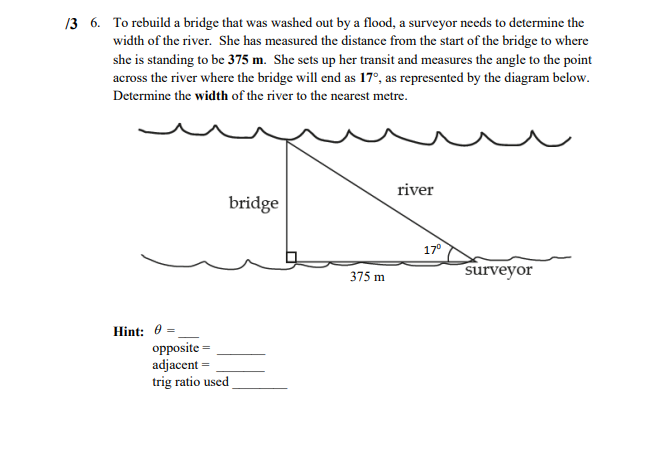
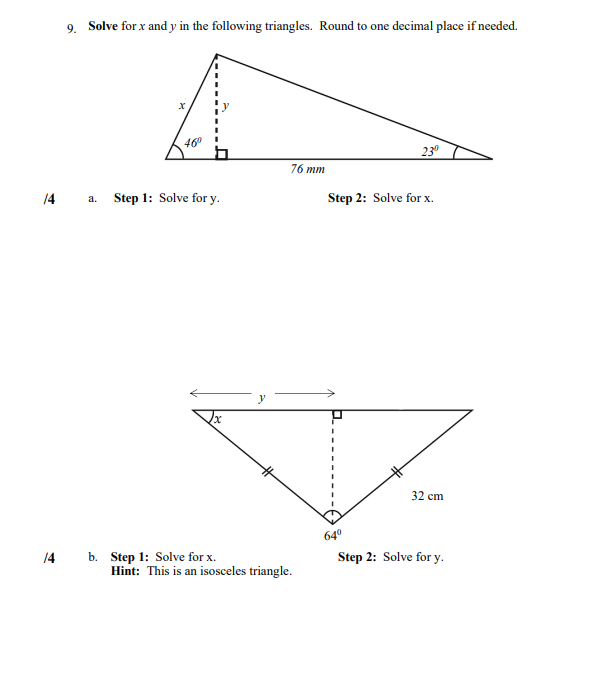
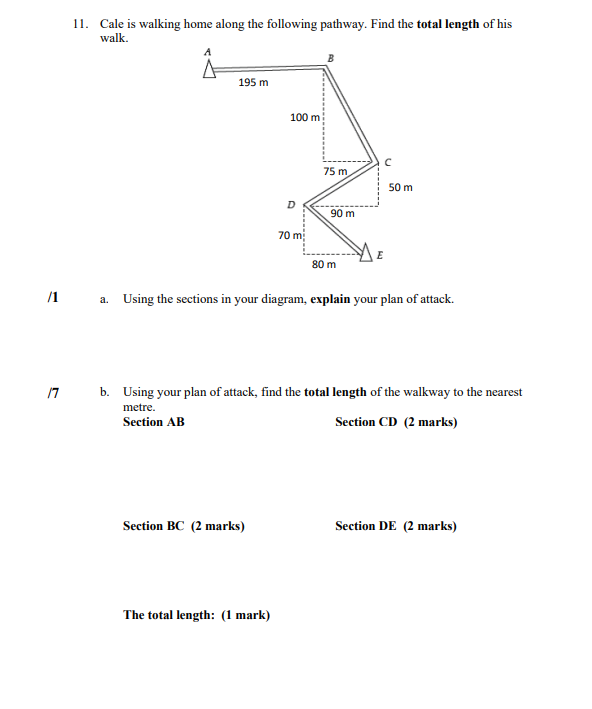
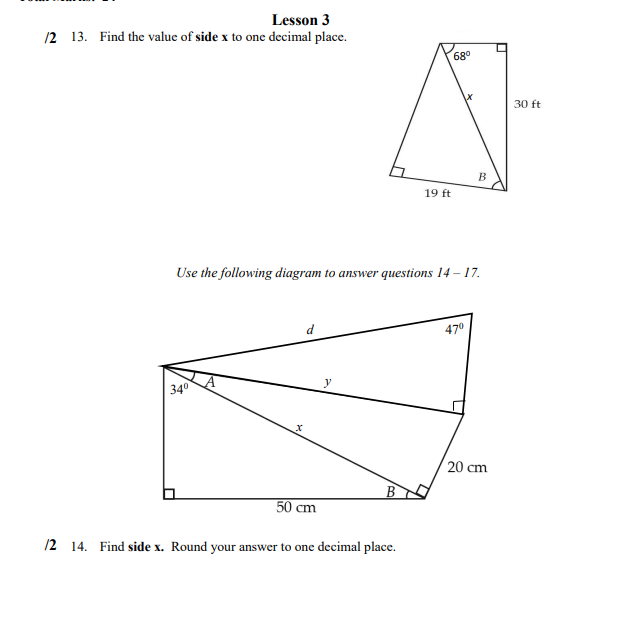
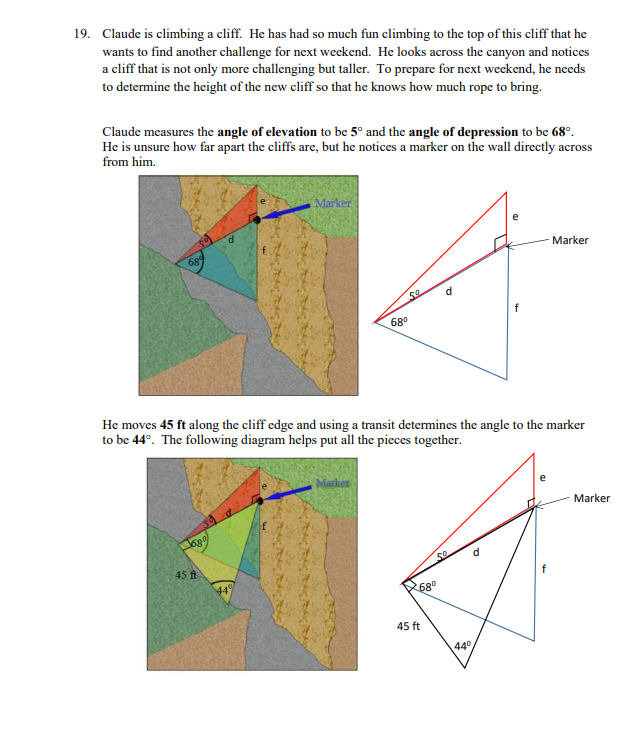
Trigonometry The Pythagorean Theorem c =atb Trig Ratios sin 0 = opp hyp Opposite Side Hypotenuse Side (hyp) adj (opp) COSO = hyp Adjacent Side tan 0 = opp (adj) adj Sum of the Angles in a Triangle 0, + 0, +0, =180" or ZA+ ZB+ ZC=180"Lesson 1 /3 1. Find angle x. Round your answer to the nearest degree. Hint: 0 = opposite = adjacent = trig ratio used 8 m Remember you will need to use your inverse function on your calculator to find the angle. 12 m /3 2. Find the value of side x to the nearest tenth. Hint: 8 = opposite = adjacent = 7.3 m trig ratio used/2 3. Describe at least two ways you could solve for the missing side, x, in the following triangle. 15 ft 8 fi X 510 2. (3 4. A ramp is attached to a mover's truck. The ramp is 7 ft long and the truck is 6 ft from the bottom of the ramp. A diagram of the ramp with dimensions is below. 7 ft I 6 ft To the nearest degree, determine the angle that the ramp makes with the ground. Hint: 0 = adjacent = hypotenuse = trig ratio used Remember you will need to use your inverse function on your calculator to find the angle.5. Solve the following right triangle for the labelled unknowns. Round your answers to one decimal place if necessary. A 87 mm X 270 13 Step 1: Solve for x. Hint: 0 = opposite = hypotenuse = trig ratio used 13 Step 2: Solve for y. Hint: 0 = adjacent = hypotenuse = trig ratio used /1 Step 3: Solve for A to the nearest degree. Hint: The known 0 = This is a right triangle so the second angle is 0, + 0, + 0, =180'/3 6. To rebuild a bridge that was washed out by a flood, a surveyor needs to determine the width of the river. She has measured the distance from the start of the bridge to where she is standing to be 375 m. She sets up her transit and measures the angle to the point across the river where the bridge will end as 17, as represented by the diagram below. Determine the width of the river to the nearest metre. river bridge 170 375 m surveyor Hint: 0 = opposite = adjacent = trig ratio used/2 7. The world's largest totem pole is located on the northern end of Cormorant Island, BC. While on the ferry to see the totem pole, you decide to try to use your knowledge from Math 20-3 class to determine how tall the totem pole is. The captain of the ferry tells you that the ferry is 500 m away from the totem pole. You determine that the angle made with the water to the top of the totem pole is 6. A diagram of the situation is given below. X 500 m Determine how tall the totem pole is. Round your answer to the nearest metre.Trigonometry The Pythagorean Theorem c' =a'+ b' Trig Ratios sin 0 = opp hyp Hypotenuse Side Opposite Side (hyp) adj (opp) cos U = hyp tan 0 =. opp Adjacent Side (adj) adj Sum of the Angles in a Triangle 0, + 0, +0, =180 or ZA+ ZB+ZC=180Answer the following questions, showing all your work for full marks. You may ask for clarification from your teacher, but you will not be given the answer. Total Marks: 31 Lesson 2 8. Using one line, construct two right triangles in these non-right triangles. Indicate the location of the 90 angles with squares. /1 a /1 b.9. Solve for x and y in the following triangles. Round to one decimal place if needed. 460 230 76 mm /4 a. Step 1: Solve for y. Step 2: Solve for x. V x 32 cm 640 14 b. Step 1: Solve for x. Step 2: Solve for y. Hint: This is an isosceles triangle.10. Use the diagram to answer the questions below. T 21 mm /220 1 70 M 32 mm W /1 a. Plan of attack: Explain how you are going to approach this question. /4 b. Solve for w. Round to one decimal place. Hint: Remember trig ratios can only be used in right angle triangles.11. Cale is walking home along the following pathway. Find the total length of his walk. 195 m 100 m: C 75 m 50 m 90 m 70 m; E 80 m /1 a. Using the sections in your diagram, explain your plan of attack. 17 b. Using your plan of attack, find the total length of the walkway to the nearest metre. Section AB Section CD (2 marks) Section BC (2 marks) Section DE (2 marks) The total length: (1 mark)12. A Canadian flag is attached to a flagpole atop the Centre Block of Parliament Hill. The top of Centre Block is six storeys high. Each storey is 5.2 metres high. From a point some distance from the Centre Block, the angle of elevation to the top of the flagpole is 54" and the angle of elevation to the bottom of the flagpole is 480. 480 A simplistic drawing of this situation is below. h2 540 48 d /2 a. Find the height, in metres from the bottom of Centre Block (the ground) to the bottom of the flagpole. Round to one decimal place. Hint: We are looking for hz./2 b. Find the distance from the bottom of Centre Block (the ground) to where the angles of elevation were taken. Round to one decimal place. Hint: Find d. 12 c. Find the height in metres from the bottom of Centre Block (the ground) to the top of the flagpole. Round to one decimal place. Hint: Find hi. /2 d. What is the height of the flagpole? Round to one decimal place. Hint: The height of the flagpole will be hs = hi - heTrigonometry The Pythagorean Theorem c' =a'+b' Trig Ratios sin 0 = opp hyp Hypotenuse Side Opposite Side (hyp) adj (opp) COSU = hyp tan 0 = opp Adjacent Side (adj) adj Sum of the Angles in a Triangle 0, + 0, +0, =180" or ZA+ ZB+ZC=180'Lesson 3 /2 13. Find the value of side x to one decimal place. 680 L 30 ft B 19 ft Use the following diagram to answer questions 14 - 17. 470 340 LA x 20 cm B 50 cm /2 14. Find side x. Round your answer to one decimal place./2 15. Find angle A. Round your answer to one decimal place. /2 16. Find side y. Round your answer to one decimal place. /2 17. Find side d. Round your answer to one decimal place.18. An airplane is 1350 ft in the air 3 miles north and 10 miles west of where it took off. Thinkstock 1350 ft d AT Take-off 3 mi 10 mi north 12 a. Determine the horizontal distance, h, the plane is from its point of take-off. Round to one decimal place Hint: Use the Pythagorean Theorem. 13 b. A person on the ground from the point of take-off looks at the plane through a clinometer. What is its angle of elevation, 47 Round to one decimal place. Hint: Convert feet to miles. 1 mi = 5280 ft/2 c. What is the airplane's straight-line distance, d, in miles, to the takeoff point? Round to one decimal place.19. Claude is climbing a cliff. He has had so much fun climbing to the top of this cliff that he wants to find another challenge for next weekend. He looks across the canyon and notices a cliff that is not only more challenging but taller. To prepare for next weekend, he needs to determine the height of the new cliff so that he knows how much rope to bring. Claude measures the angle of elevation to be 5" and the angle of depression to be 68". He is unsure how far apart the cliffs are, but he notices a marker on the wall directly across from him. Marker d Marker 50 f 680 He moves 45 ft along the cliff edge and using a transit determines the angle to the marker to be 44". The following diagram helps put all the pieces together. Marker e Marker 50 f '680 45 ft 440/2 a. Determine the distance between the two cliffs, d. Hint: Draw the triangle you will use with its dimensions. Round to one decimal place. /2 b. Determine the height of the cliff Claude is currently on, or f. Round to one decimal place. /2 c. Determine the height of the cliff Claude wants to climb next weekend, or the total of e + f. Round to one decimal place. Step 1: Find side c. Step 2: Find the total height of the new cliff. Total height = c + f/1 d. If Claude needs 20 ft extra rope for his climb, how much rope total should he bring next weekend? Round to one decimal place. Hint: We need to add 15 ft to our total from part c