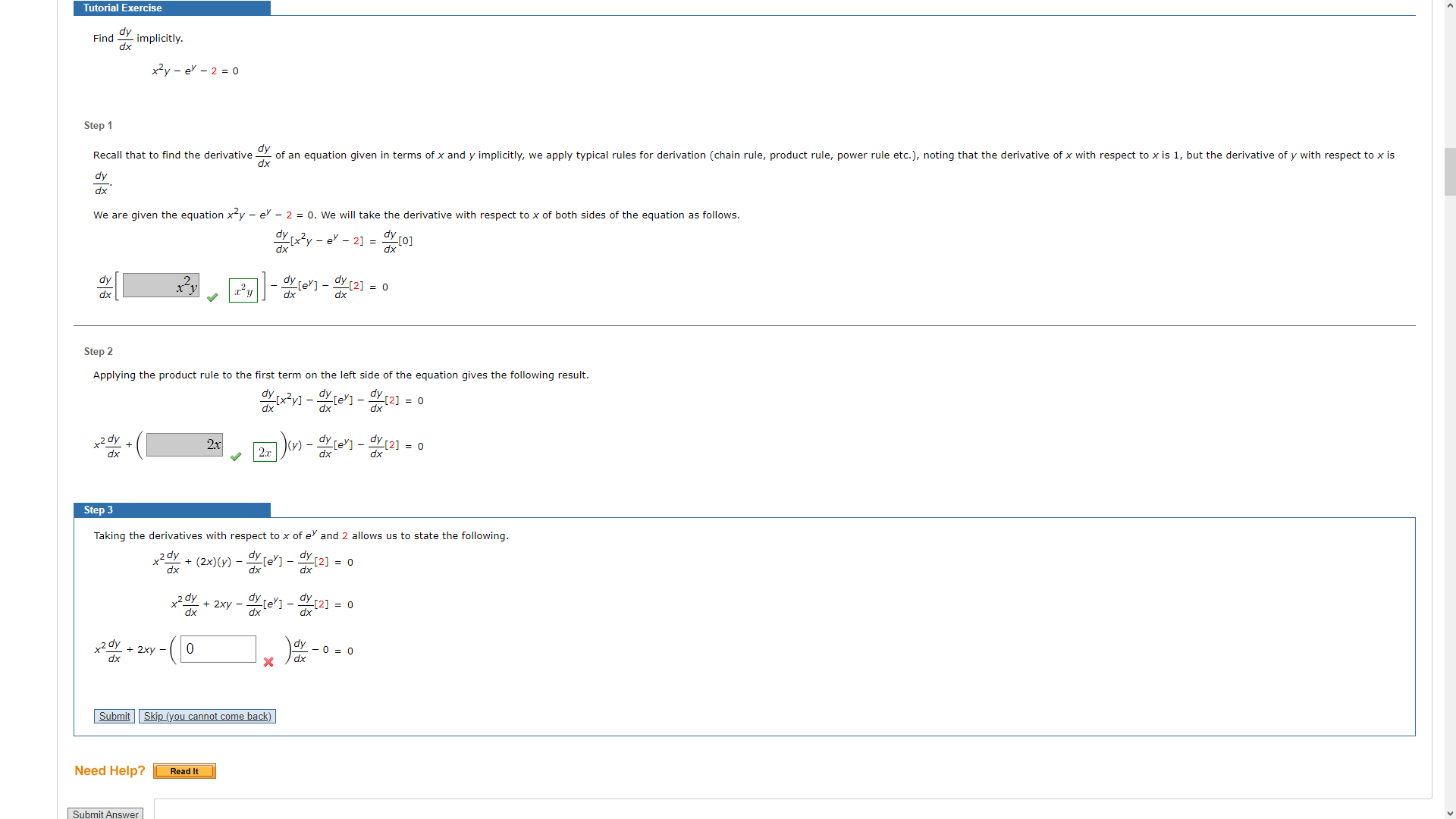
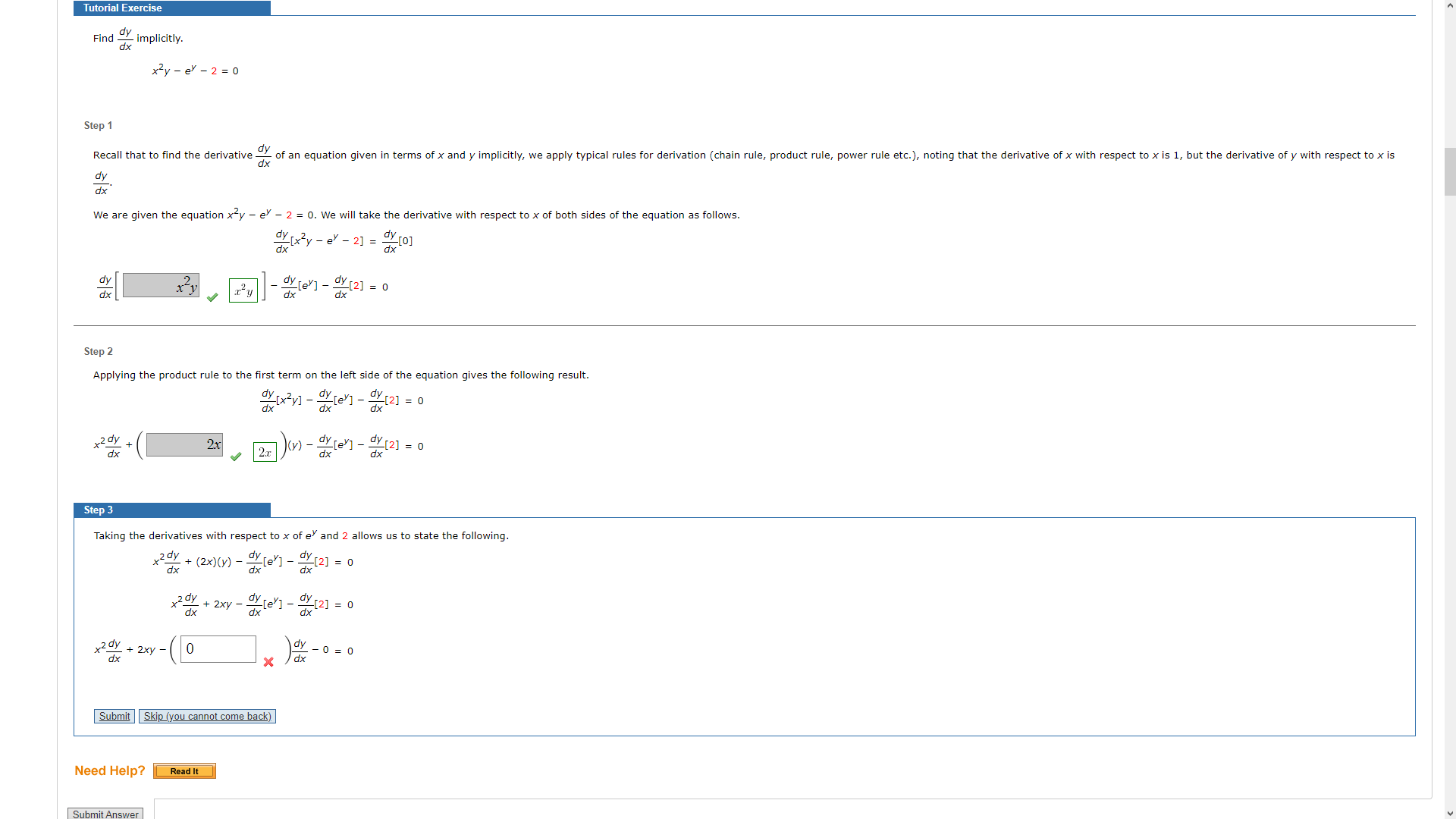
Tutorial Exercise Find ~ implicitly. dx x2 y - ey - 2 = 0 Step 1 Recall that to find the derivative - of an equation given in terms of x and y implicitly, we apply typical rules for derivation (chain rule, product rule, power rule etc.), noting that the derivative of x with respect to x is 1, but the derivative of y with respect to x is dy dx We are given the equation x y - ey - 2 = 0. We will take the derivative with respect to x of both sides of the equation as follows. dx dy [x2y - ey - 2] = [0] dx dy dx x -y 12 y dx "Y [ey] - Y[2] = 0 Step 2 Applying the product rule to the first term on the left side of the equation gives the following result. dy [ x 2 y] - - le Y [ 2 ] = 0 x2 dy 2x dy [ev] - Y [2] = 0 dx dx dx Step 3 Taking the derivatives with respect to x of e and 2 allows us to state the following. dx 2 0y + (2x) (y) - -[ey] - - [2] = 0 dx 2 0y + 2xy - - dy [ey ] - ) [2] = 0 dy dx x2 ay + 2xy 0 dy - 0 = 0 dx X dx Submit Skip (you cannot come back) Need Help? Read It