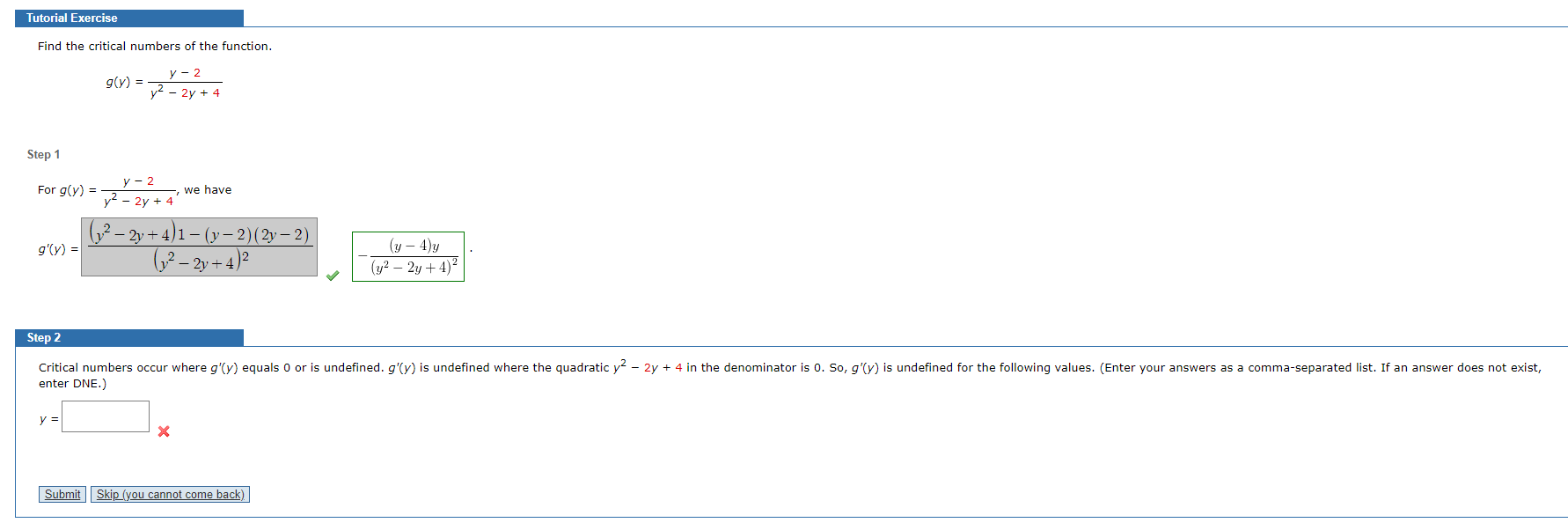
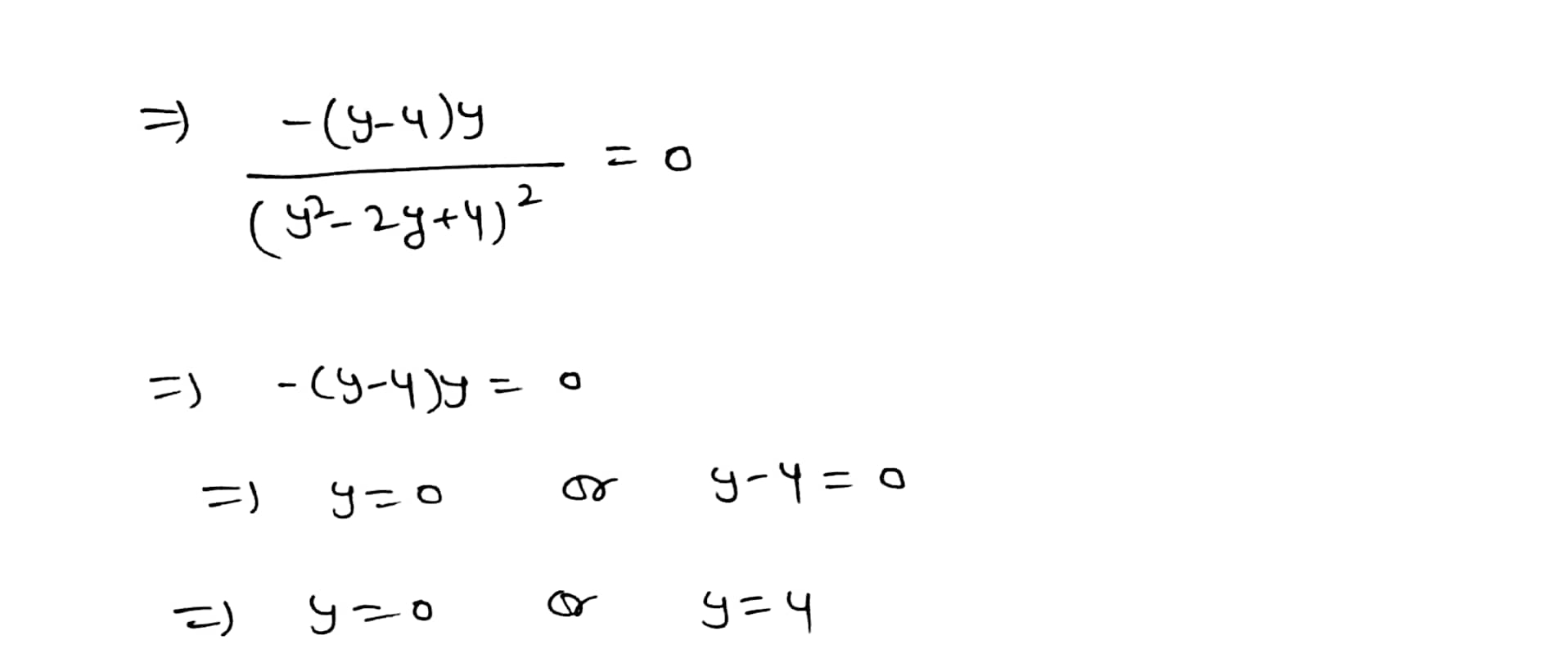
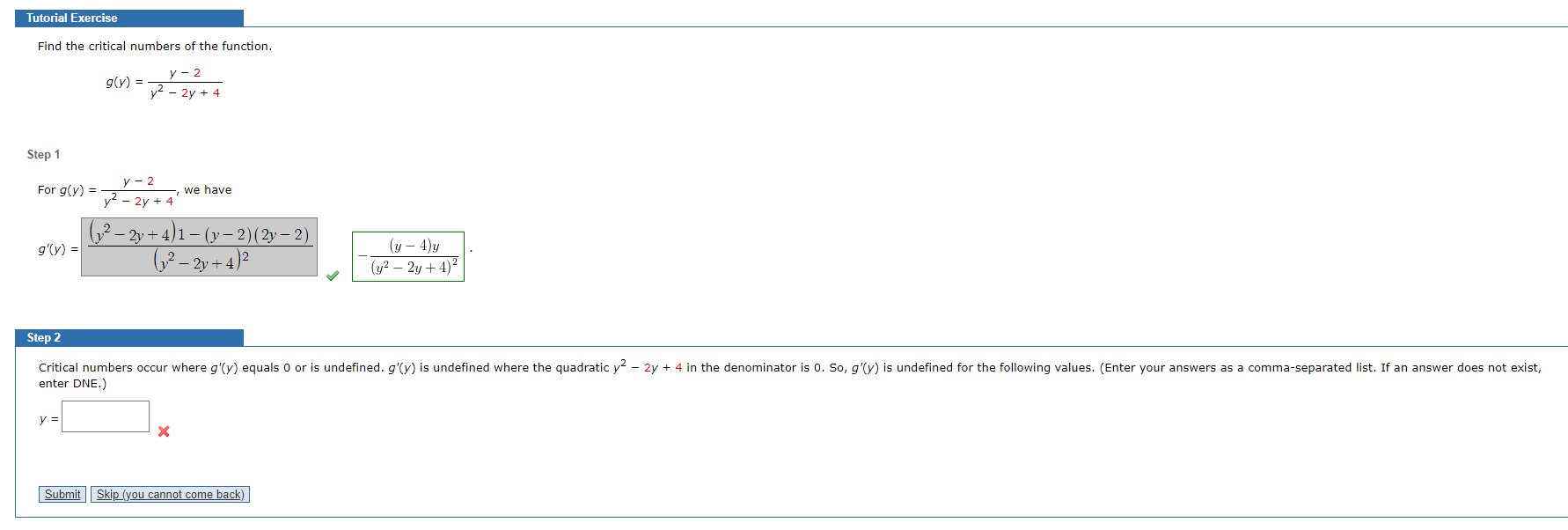
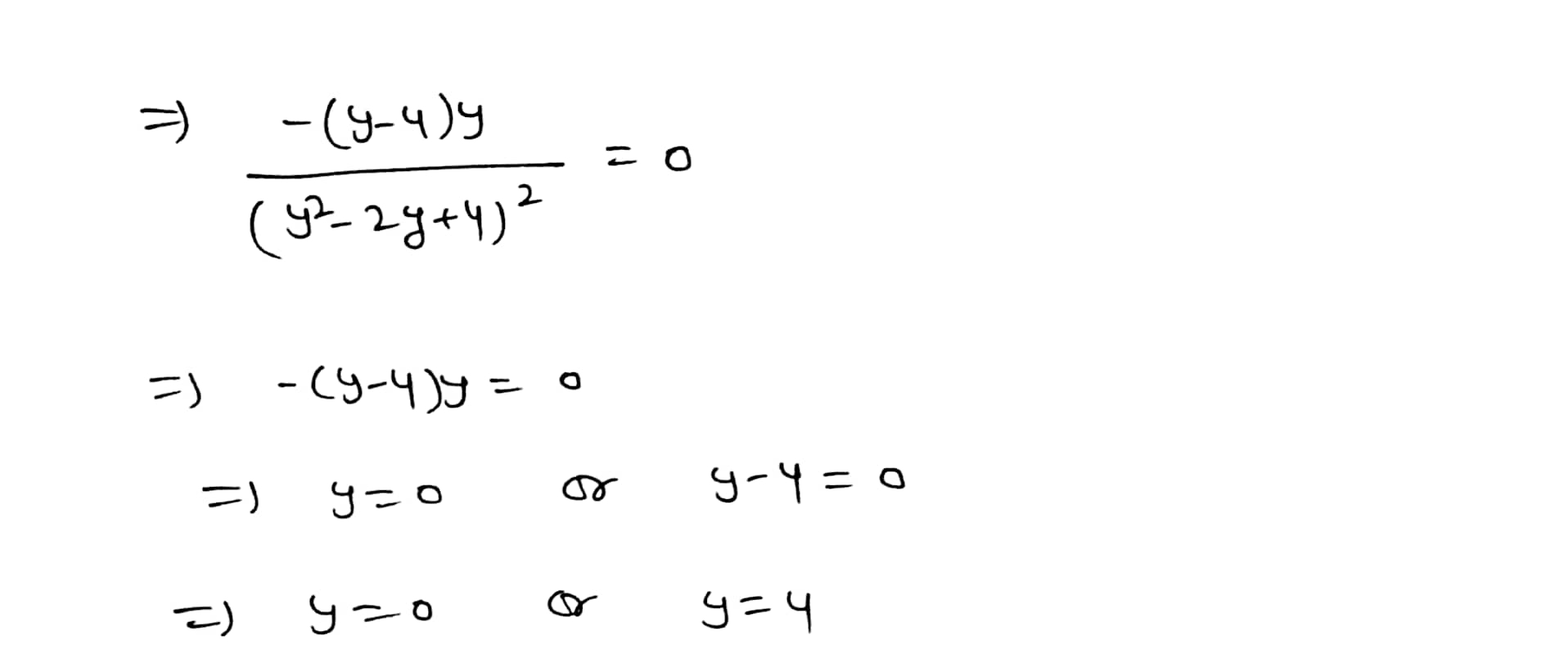
Tutorial Exercise Find the critical numbers of the function. y - 2 g ( V) = - v2 - 2y + 4 Step 1 For g(y) = y - 2 y2 - 2y + 4' -, we have 12 - 2 + 4)1 - (7-2) (2y-2) 9'()) = (y - 4)y () 2 - 27 + 4) 2 (y2 - 2y + 4)2 Step 2 Critical numbers occur where g'(y) equals 0 or is undefined. g'(y) is undefined where the quadratic y - 2y + 4 in the denominator is 0. So, g'(y) is undefined for the following values. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.) y = X Submit Skip (you cannot come back)( 4 = 2 4 + 4 ) = 0 2 4 2 2 4 + 4 = 0 - y = -(2)+ ( 2)" -4X1X4 2 =) y = 2+ 4- 16 2 7 y = 21 - 12 2 = ) y = 2+ 25-3 2 = ) y z ( +J-3 = 1+153 =) y = 1+153 or y = 1 - 153 So critical points are either yzo, y or J = 0 , 4, 1453, 1- is or y = 0, 4, 1+ J-3 , 1 - 5-3Explanation: We have given that y - 2 9 ( 4 ) = y = 24 + 4 Differentiate both sides wirt y : - y - 2 7 9 (y) = (4= 24 + 4 ) 1 - (4-2) ( 24-2) ( 4 2 2 4 + 4 ) 2 9 '( y ) = 4 - 2 y + 4 - 24 + 2 4 + 4y-4 ( 8 2 - 2 y +4 ) 2 1 9 ' ( y ) = - y + 44 - ( 9- 4 ) y ( 4 - 2 8 + 4 ) 2 ( 4 2 - zy + 4 1 2 For critical numbery: g ( y ) = 0 or ( y = zy ty ) = d- (4- 4 ) y ( SP - 24 + 4 ) 2 = ) - (y-4)y = 0 = ) y =0 y - y = 0 = ) y = 4