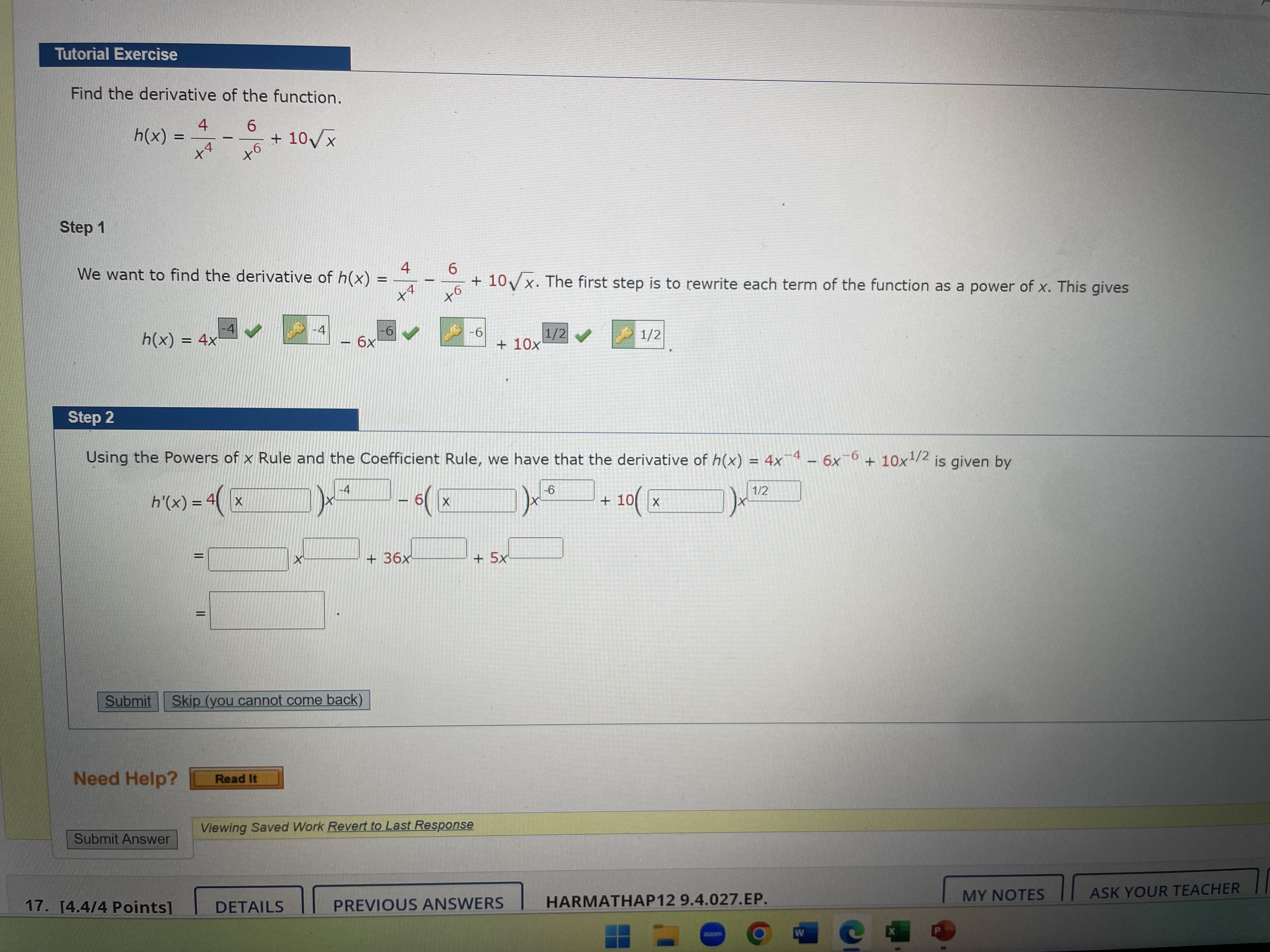
Question: Tutorial Exercise Find the derivative of the function. h(x)=(4)/(x^(4))-(6)/(x^(6))+10sqrt(x) Step 1 We want to find the derivative of h(x)=(4)/(x^(4))-(6)/(x^(6))+10sqrt(x) . The first step is
Tutorial Exercise\ Find the derivative of the function.\
h(x)=(4)/(x^(4))-(6)/(x^(6))+10\\\\sqrt(x)\ Step 1\ We want to find the derivative of
h(x)=(4)/(x^(4))-(6)/(x^(6))+10\\\\sqrt(x). The first step is to rewrite each term of the function as a power of
x. This gives\
h(x)=4x^(-4)\\\\sqrt(-4-6)+10x^((1)/(2))\ Step 2\ Using the Powers of
xRule and the Coefficient Rule, we have that the derivative of
h(x)=4x^(-4)-6x^(-6)+10x^((1)/(2))is given by\
Find the derivative of the function. h(x)=x44x66+10x Step 1 We want to find the derivative of h(x)=x44x66+10x. The first step is to rewrite each term of the function as a power of x. This gives h(x)=4x46x6+10x1/21/2 Step 2 Using the Powers of x Rule and the Coefficient Rule, we have that the derivative of h(x)=4x46x6+10x1/2 is given by h(x)=4()x6+6()x6+10(=x+36x+5x Viewing Saved Work Revert to Last Response
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


