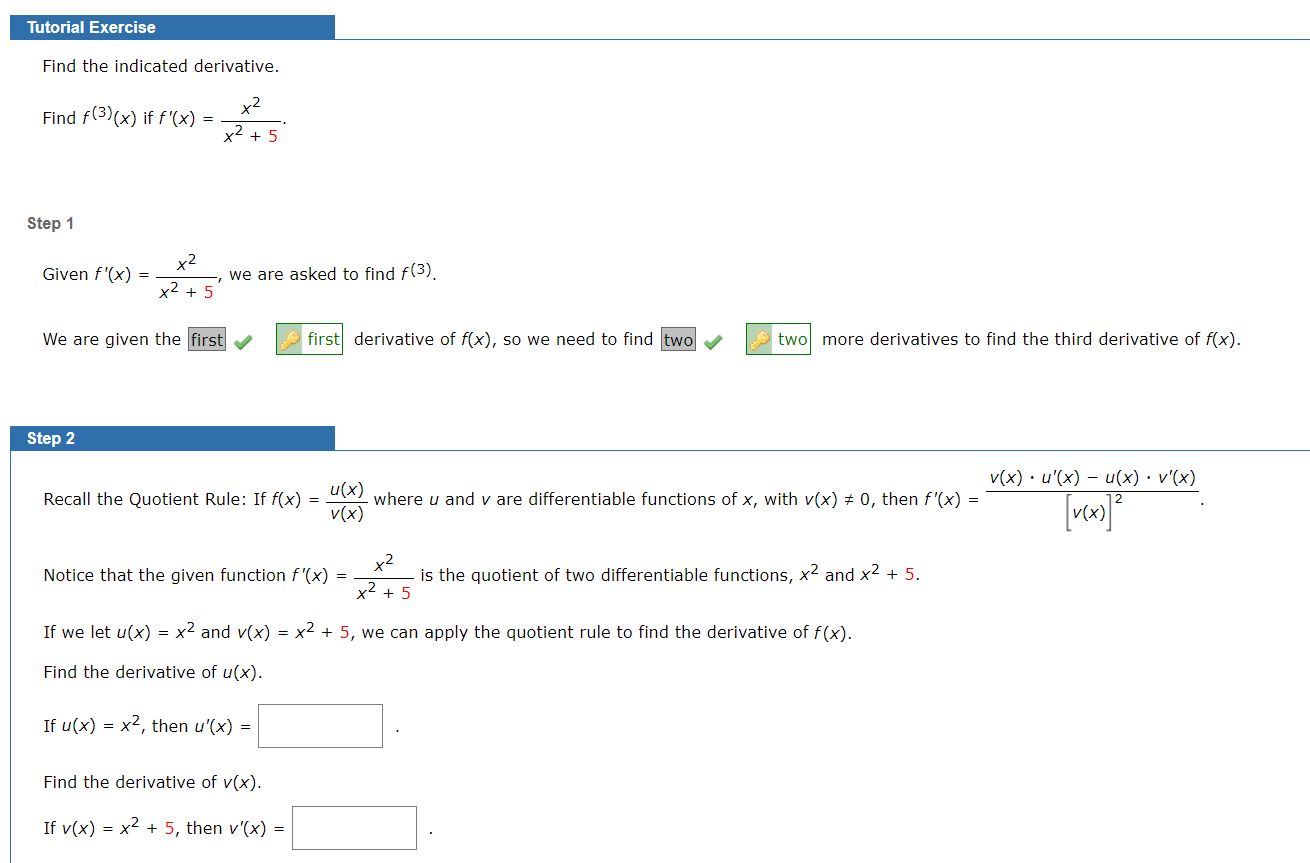
Tutorial Exercise Find the indicated derivative. X2 Find f(3)(x) if f'(x) = x2+5 Step 1 X2 Given f'(x) : , we are asked to find H3). x2+5 We are given the first y J first derivative of x], so we need to find two y .2 two more derivatives to find the third derivative of f(x]. v(x) - u'[x) u(x) - v'(x) Recall the Quotient Ruie: If for) = \"EX; where u and v are differentiable functions of X, with v(x) i 0, then f'(x) = [v(x)]2 v x 2 Notice that the given function f'(x] = 2 is the quotient of two differentiable functions, X2 and X2 + 5. X + 5 If we let u(x) = x2 and V(X) = X2 + 5, we can apply the quotient rule to find the derivative of x]. Find the derivative of u(x). If u(x) = x2, then u'(x) = Find the derivative of v(x). If v(x) = X2 + 5, then v'(x) =