Two graphs G and H are isomorphic (written GH or GH) if there exist bijections

:V(G)V(H) and :E(G)E(H) such that vV(G) is incident with eE(G) precisely when (v)V(H) is incident with (e)E(H) .

We can check whether two graphs are isomorphic by asserting that one is a consistent relabelling of the other.

In the diagrams below, the positions of the vertices can be changed by clicking and dragging them.

To prove two graphs are isomorphic, we can provide a bijective mapping between the two vertex sets. Find such a function for the following two graphs.

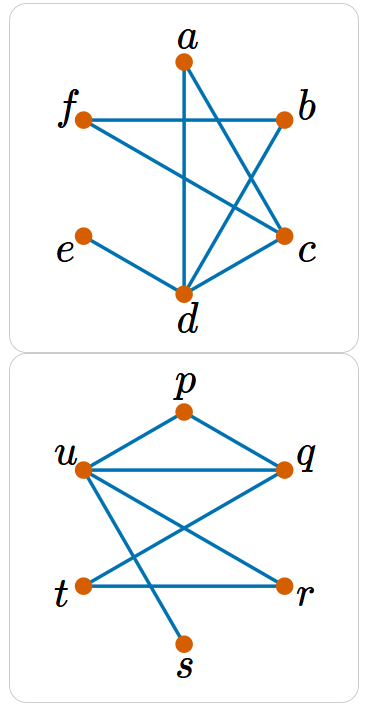
\f