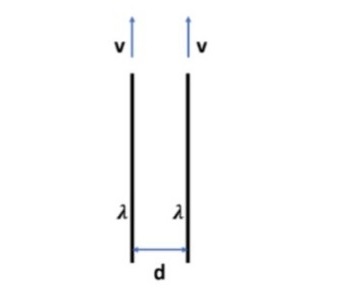
Two infinitely long load lines are parallel and both carry a linear charge density ?. They are separated by a distance d. Now consider that these two lines of charges move at a constant speed v in the same direction (z-direction). They are found in a vacuum (?0 = 8.85 x 10^-12 F/m; ?0 = 4? x 10^-7 H/m). a. The two lines of charges will repel each other because of their electrostatic interaction. Determine an expression for the magnitude of the electrostatic force per unit of length felt by each of the load lines. b. As the lines of charges move, you can determine the current as I = dQ/dt = ?dl/dt = ?v. Find an expression for the magnetic flux density B induced by one of the charge lines at a distance d from it. C. These two lines of charges will attract each other due to magnetic forces. Find an expression for the magnitude of the magnetic force per unit length felt by the load lines. d. The magnetic force calculated in (c) depends on the speed. Show that the two lines of charges must move at exactly the speed of light (approximately 3 10^8 m/s) for the force of magnetic attraction to completely counteract the electrostatic repulsion force. e. Marvel at this incredible result!