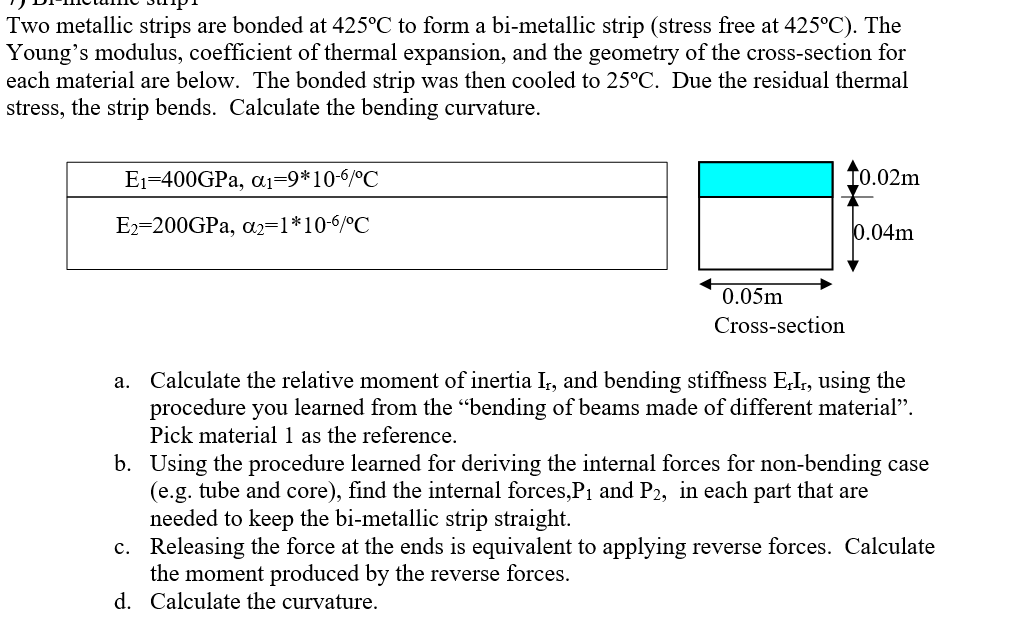
Question: Two metallic strips are bonded at ( 4 2 5 ^ { circ } mathrm { C } ) to form
Two metallic strips are bonded at circmathrmC to form a bimetallic strip stress free at circmathrmC The Young's modulus, coefficient of thermal expansion, and the geometry of the crosssection for each material are below. The bonded strip was then cooled to circmathrmC Due the residual thermal stress, the strip bends. Calculate the bending curvature.
a Calculate the relative moment of inertia mathrmImathrmr and bending stiffness mathrmEmathrmrmathrmImathrmr using the procedure you learned from the "bending of beams made of different material". Pick material as the reference.
b Using the procedure learned for deriving the internal forces for nonbending case eg tube and core find the internal forces, mathrmP and mathrmP in each part that are needed to keep the bimetallic strip straight.
c Releasing the force at the ends is equivalent to applying reverse forces. Calculate the moment produced by the reverse forces.
d Calculate the curvature.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


