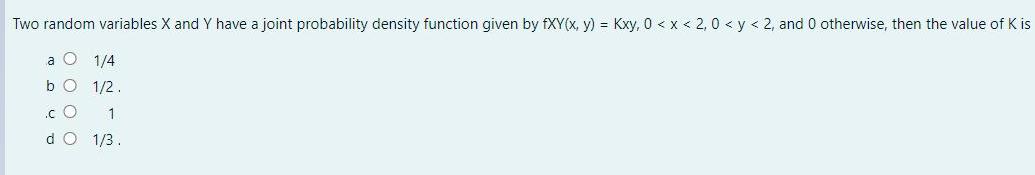
Two random variables X and Y have a joint probability density function given by fXY(x, y) = Kxy, 0 < x < 2, 0 < y < 2, and 0 otherwise, then the value of K is 1/4 b O 1/2. 1 d O 1/3. A random process X(t) is given by X(t) = A sin(wt + 0), where A is a uniformly distributed random variable with mean E[A] and variance VAR(A). Then, the mean value of X(t) is 31 J E[A] .a O 0 1.0 E[A] sin(wt + 0).b O sin(wt) .c O lia ale P 1/2 .d O