Question: Two simple pendulums with equal lengths ( L = 0 . 9 5 6 m ) and masses ( m = 0 . 4 2
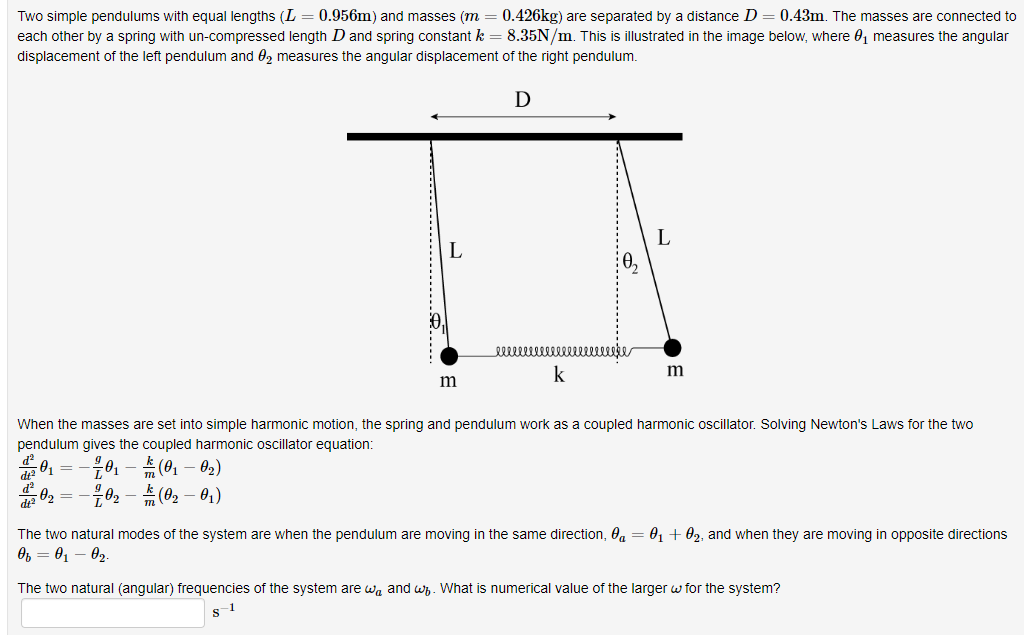
Two simple pendulums with equal lengths and masses are separated by a distance The masses are connected to
each other by a spring with uncompressed length and spring constant This is illustrated in the image below, where measures the angular
displacement of the left pendulum and measures the angular displacement of the right pendulum.
When the masses are set into simple harmonic motion, the spring and pendulum work as a coupled harmonic oscillator. Solving Newton's Laws for the two
pendulum gives the coupled harmonic oscillator equation:
The two natural modes of the system are when the pendulum are moving in the same direction, and when they are moving in opposite directions
The two natural angular frequencies of the system are and What is numerical value of the larger for the system?
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


