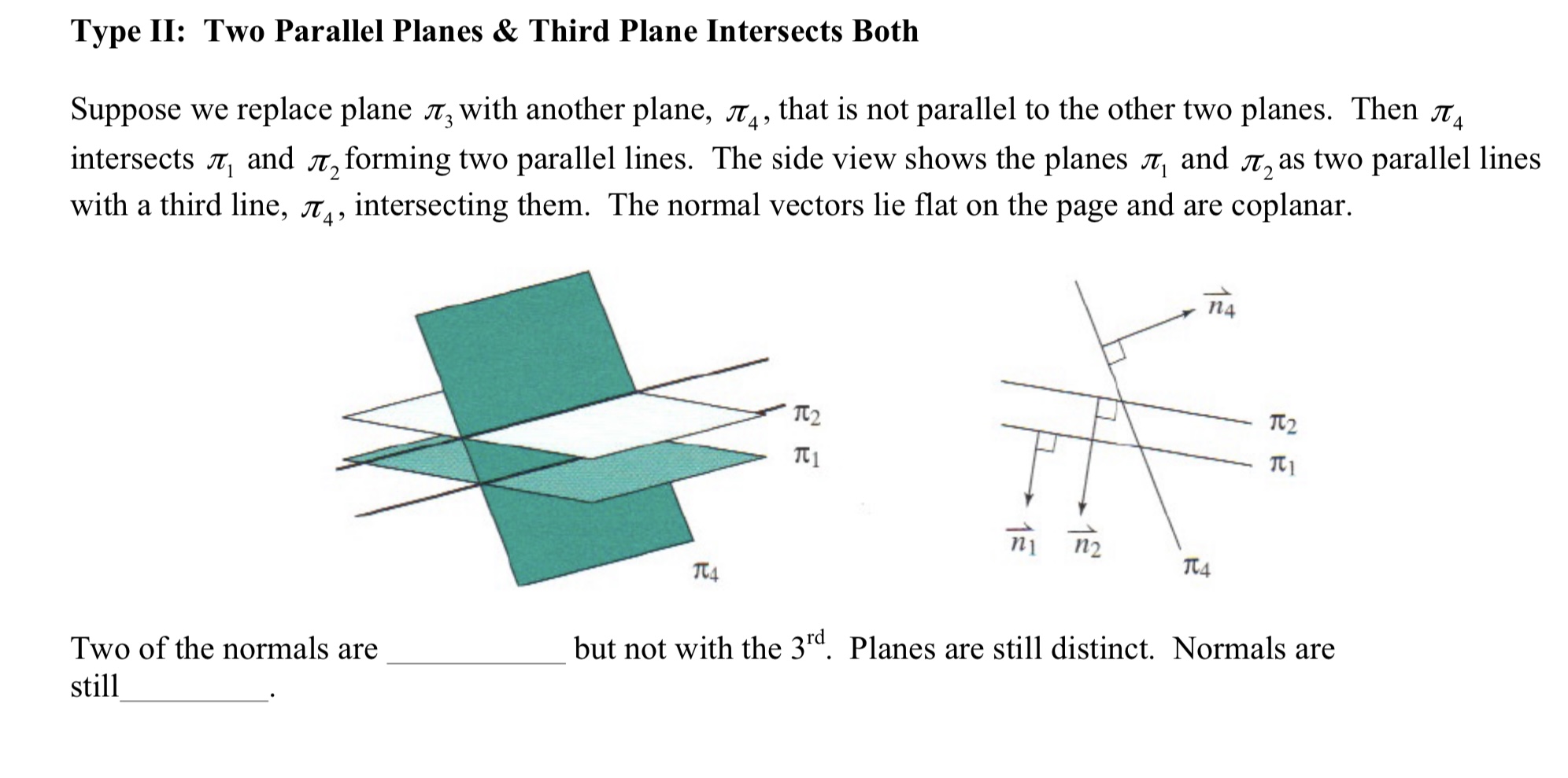
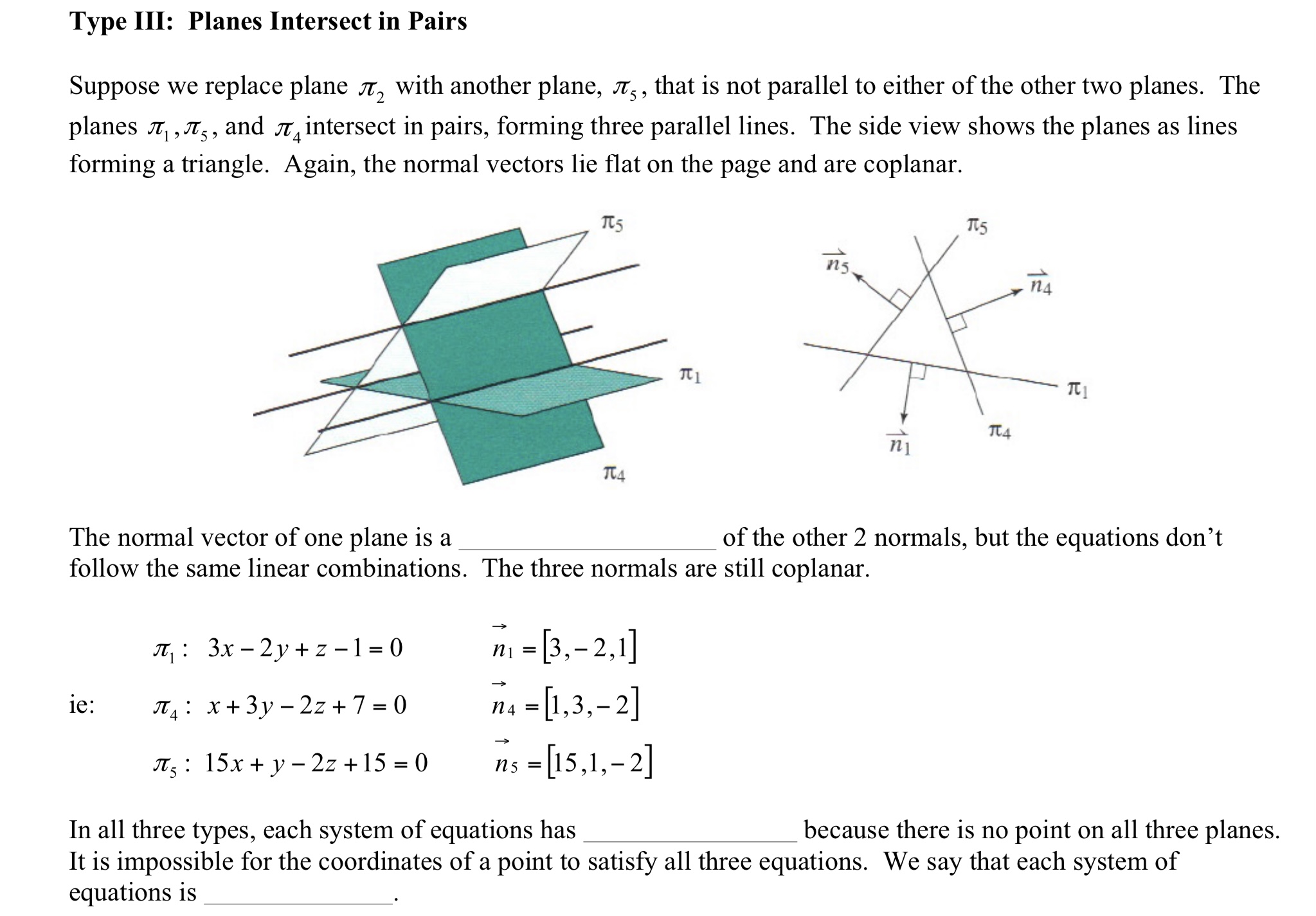
Type II: Two Parallel Planes & Third Plane Intersects Both Suppose we replace plane as with another plane, n4 , that is not parallel to the other two planes. Then :14 intersects .731 and .712 forming two parallel lines. The side View shows the planes 1:1 and 11:2 as two parallel lines with a third line, 34 , intersecting them. The normal vectors lie at on the page and are coplanar. i; 1'2 Th 7a? 7'2 n4 Two of the normals are but not with the 3rd. Planes are still distinct. Normals are still Type III: Planes Intersect in Pairs Suppose we replace plane :12 with another plane, .71'5 , that is not parallel to either of the other two planes. The planes 17:1,.71'5 , and :14 intersect in pairs, forming three parallel lines. The side View shows the planes as lines forming a triangle. Again, the normal vectors lie at on the page and are coplanar. TE5 \"5 7's _. n4 1C1 TE] __ n4 \"1 The normal vector of one plane is a of the other 2 normals, but the equations don't follow the same linear combinations. The three normals are still coplanar. :11: 3x2y+zl=0 n1=[3,2,l] ie: .714: x+3y2z+7=0 n4=[l,3,2] H5215x+y-22+15=0 ns=[15,1,2] In all three types, each system of equations has because there is no point on all three planes. It is impossible for the coordinates of a point to satisfy all three equations. We say that each system of equations is The normal vector of one plane is a of the other 2 normals, but the equations don't follow the same linear combinations. The three normals are still coplanar. > m: 3x2y+z1=0 n1=[3,2,1] ie: .714: x+3y22+7=0 ;4=[1,3,2] its: 15x+y22+15=0 n5 =[15,1,2] In all three types, each system of equations has because there is no point on all three planes. It is impossible for the coordinates of a point to satisfy all three equations. We say that each system of equations is Example # 1: Describe how the planes in each linear system are related, If there is a unique point or line of intersection, detennine its coordinates or equation. .7512 x+y+z+5=0 a) n2: x+2y+3z+4=0 J13: x+y+z=0