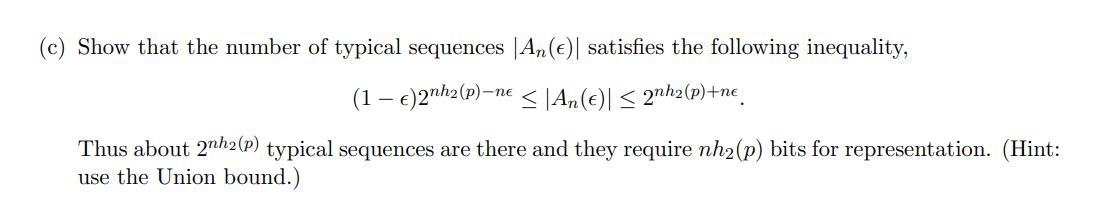
(Typical sets) Let X, X2,..., Xn be i.i.d. Bernoulli(p) random variables. Let p(x), x = 0, 1 be the pmf of X. Consider the typical set, An () := { x : | - = log,(P(17)) H(p)| e}. n (a) Show that for any fixed > 0 and large enough n, P((X, X2, ..., Xn) An ()) (1 ). (b) Let h(p) = -plog p- (1-p) log2 (1-p). Show that for any (x1,...,xn) An (), 2-nh2(p)-ne P((X, ..., Xn) = (x,...,xn)) 2-nh(p)+ne Thus, all typical set sequences have approximately the same probability of 2-nh2(p). (c) Show that the number of typical sequences An(e)| satisfies the following inequality, (1 - )2nh2(p)-ne |An()| 2nh2(p)+ne Thus about 2nh2(p) typical sequences are there and they require nh (p) bits for representation. (Hint: use the Union bound.)