Question: u =7x 1 + 2 Let y = y = du. Use the Fundamental Theorem of Calculus to find y'. (1 point) Let F(x)

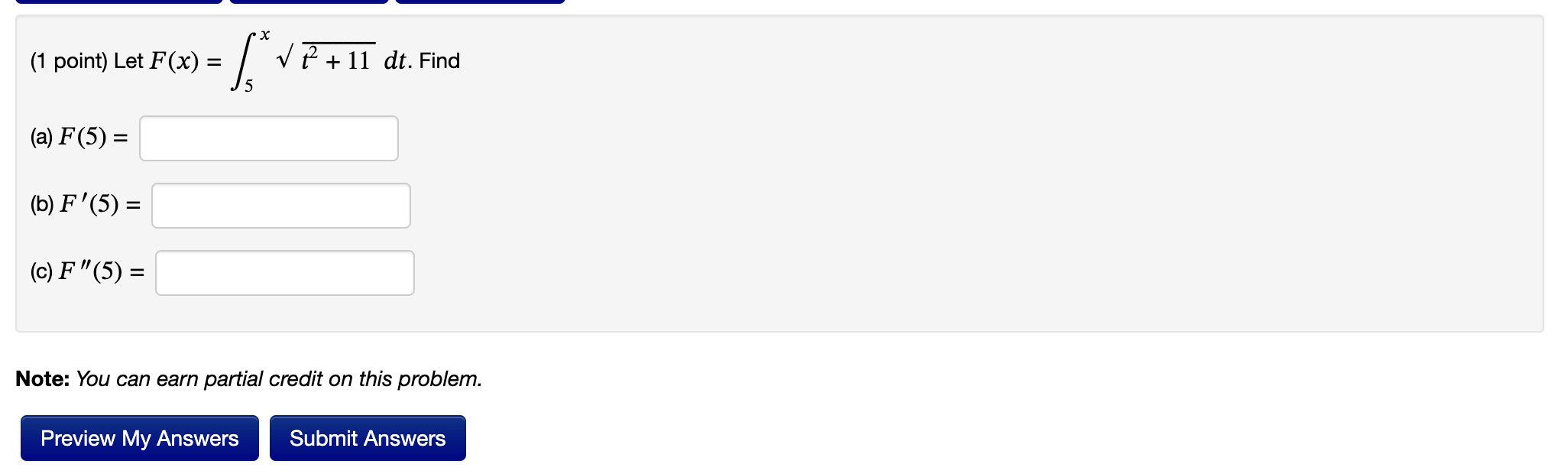
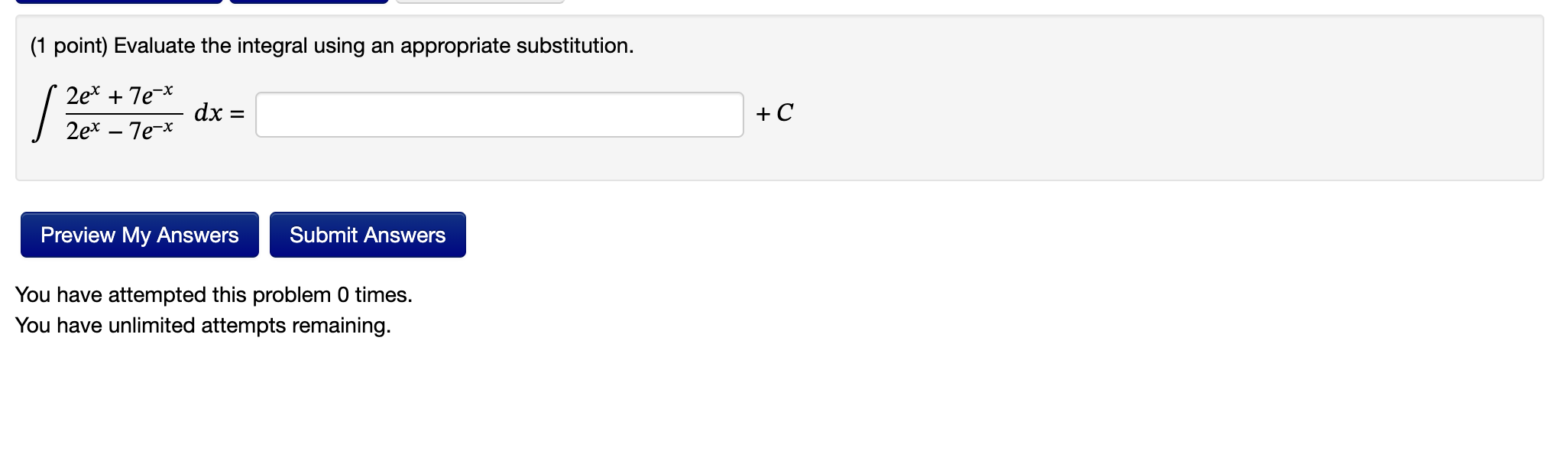
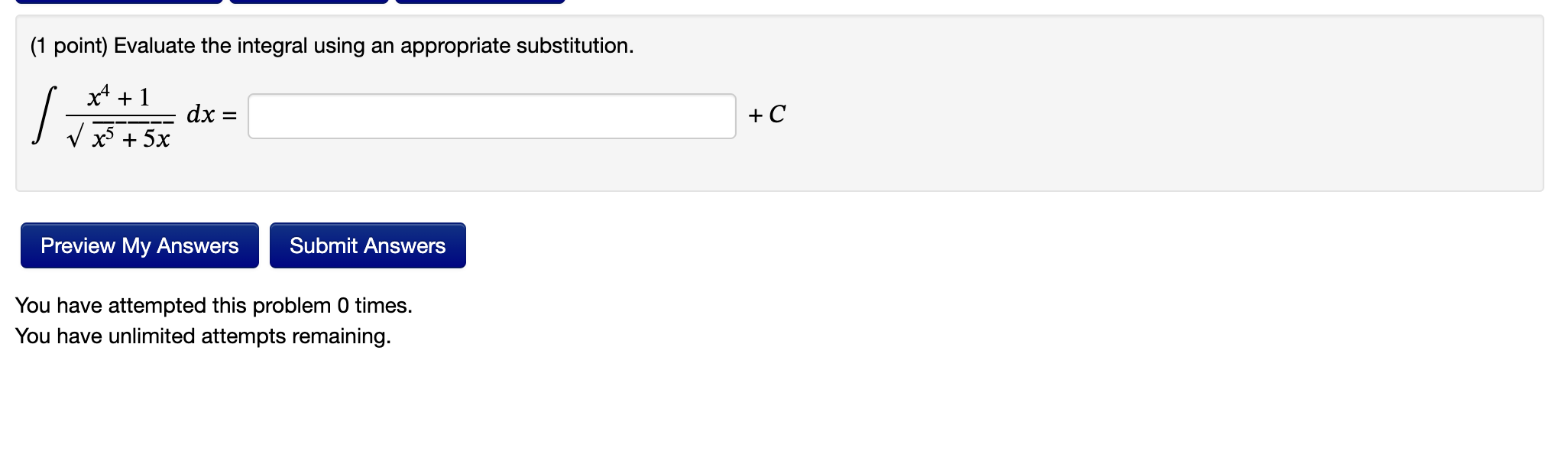
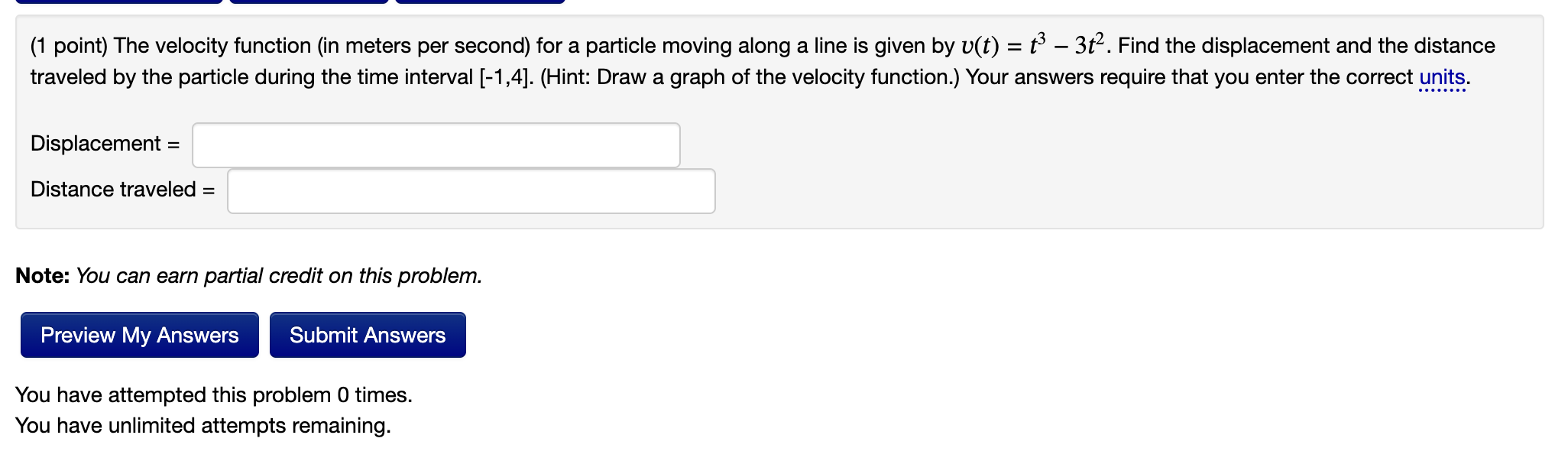
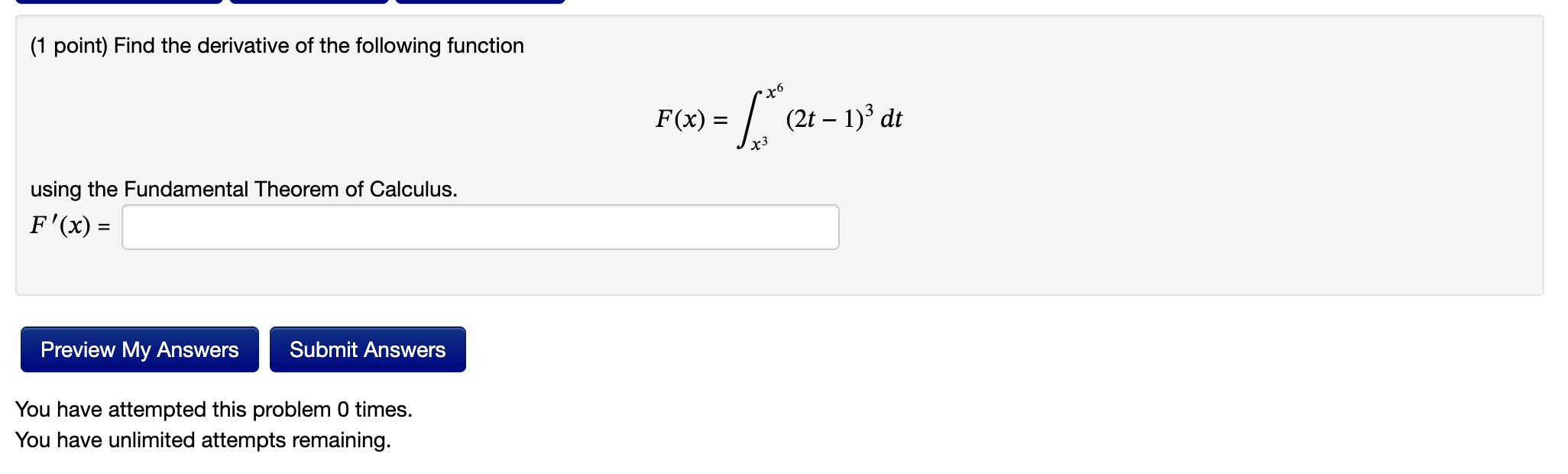
u =7x 1 + 2 Let y = y = du. Use the Fundamental Theorem of Calculus to find y'. (1 point) Let F(x) = (a) F (5) = (b) F'(5) = (c) F"(5) = X fr 5 + 11 dt. Find Note: You can earn partial credit on this problem. Preview My Answers Submit Answers (1 point) Evaluate the integral using an appropriate substitution. 2ex + 7e-x se e 2ex - 7e-x dx = Preview My Answers Submit Answers You have attempted this problem 0 times. You have unlimited attempts remaining. + C (1 point) Evaluate the integral using an appropriate substitution. x + 1 / x5 + 5x dx: = Preview My Answers Submit Answers You have attempted this problem 0 times. You have unlimited attempts remaining. + C (1 point) The velocity function (in meters per second) for a particle moving along a line is given by v(t) = t 3t. Find the displacement and the distance traveled by the particle during the time interval [-1,4]. (Hint: Draw a graph of the velocity function.) Your answers require that you enter the correct units. Displacement = Distance traveled = Note: You can earn partial credit on this problem. Preview My Answers Submit Answers You have attempted this problem 0 times. You have unlimited attempts remaining. (1 point) Find the derivative of the following function using the Fundamental Theorem of Calculus. F'(x) = Preview My Answers Submit Answers You have attempted this problem 0 times. You have unlimited attempts remaining. x6 = [ (2 x3 F(x) = (2t - 1) dt

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

1 If y 2 Let 3 O 5 17X 8 y 756x 56x 7 U3 1463 5 Theu F5 5 F 5 Fx SVE 711 2 e 1 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function. 8. g(x) = (" In t dt 7. g(x) = VT+ 21 dt sin t dt dx 10. glu) = 9. g(y) 11. F(x) = cos(r) dt Hint: [" costr?)...

practice exception handling via catching or throwing the exception. Recall that we catch exceptions via surrounding the exception with a try/catch block. If we cannot catch the exception then we need...

(i) Write down the linear program relaxation for the vertex cover problem and solve the linear program. [6 marks] (ii) Based on the solution of the linear program in (b)(i), derive an integer...

Artculos indefinidos. Complete the following sentences with the correct indefinite article (2 points each, 10 points total). Carolina es ___________ chica latinoamericana. Argentina es _____________

Problem 1. (1 point) Problem 4. (1 point) Part 1 of 2: Find a function f and a number a such that This is a multi-part problem. If F() = 2+2 + 5t, find F'(). It 2 dt = 2vx FOE for all x > 0....

1. Suppose that for a certain leafcutter ant colony, the birth rate is modelled by: t B(t) = 23, 000 805111 (7%) ants per day and the death rate is modelled by: D(t) = 21, 000 30 cos(37rt) ants per...

Results for this submission Entered Answer Preview Result (40963 + 1536x2 - 192r + 8) -[4096*(X*3)+1536"(x*2)-192"x+8]/([(1-8*x)^2]+1) incorrect (1 - 8x)+1 The answer above is NOT correct. (1 point)...

CONCORDIA UNIVERSITY Department of Mathematics & Statistics Course Number Mathematics 205 Examination Date Final April 2017 Instructors: J. Bernatska, A. Boyarsky, L. Colo, S. Link, E. H.-M. Ng...

What happens after a cell becomes a cancer cell?

Use the n-IG system state TESTcalc to (a) determine the chemical potential (k) of hydrogen in an equimolar mixture of hydrogen and carbon dioxide at 100 kPa and 300 K. Plot how the chemical potential...

Convert the point from rectangular coordinates t o spherical coordinates. ( - 5 , - 5 , 2 2 ) ( , , ) = Need Help?

The DoorRed pharmacy has 25 retail outlets in the Chicago region. The current policy is to carry every drug in each retail outlet. DoorRed is investigating the possibility of centralizing some of the...

Elements from the adjusted trial balance for Maggie Co., a retailer, for the fiscal year end (12/31) 2015 are: Accounts Receivable $555,000 Accumulated Depr.-equipment 450,000 Accumulated...

We explore several techniques for allocation costs. Let's pretend you are on a committee to determine how much much tuition should increase per student for an upgrade in computer technology. For...

Keele Bank has the following items on its balance sheet (expressed in $billion). ESF 2 Accumulated retained profit 54 Term Deposits of customers 630 Loans to households 500 Capital notes on issue 4...

You are the internal audit senior responsible for conducting an assurance engagement of the XYZ Company payroll process. This process has not been audited for three years and, as such, is due in the...

The fixed costs for manufacturing hand - painted wooden decorative plaques are $ 7 , 0 0 0 . The 5 inch oval plaques Are sold at craft stores for $ 4 . 5 0 each Variable costs to produce 1 0 0...

A water trough is 10 m long and a cross-section has the shape of an isosceles trapezoid that is 30 cm wide at the bottom, 80 cm wide at the top, and has height 50 cm. If the trough is being filled...

(a) Set up an integral for the area of the surface obtained by rotating the curve about (i) the -axis and (ii) the -axis. (b) Use the numerical integration capability of your calculator to evaluate...

Find the linear approximation of the function f(x) = 1 - x at a = 0 and use it to approximate the numbers 0, 9 and 0.99. Illustrate by graphing f and the tangent line.

Let the time (in weeks) from shipment of a defective product until the customer returns the product. Suppose that the minimum return time is and that the excess g 5 3.5 1021 X 5 a 5 2.5 b 5 200 P(1.5...

The article On Assessing the Accuracy of Offshore Wind Turbine Reliability-Based Design Loads from the Environmental Contour Method (Intl. J. of Offshore and Polar Engr., 2005: 132140) proposes the...

Evaluate the following: a. (6) b. (5/2) c. F(4; 5) (the incomplete gamma function) d. F(5; 4) e. F(0 ; 4)