U S E M A T L A B

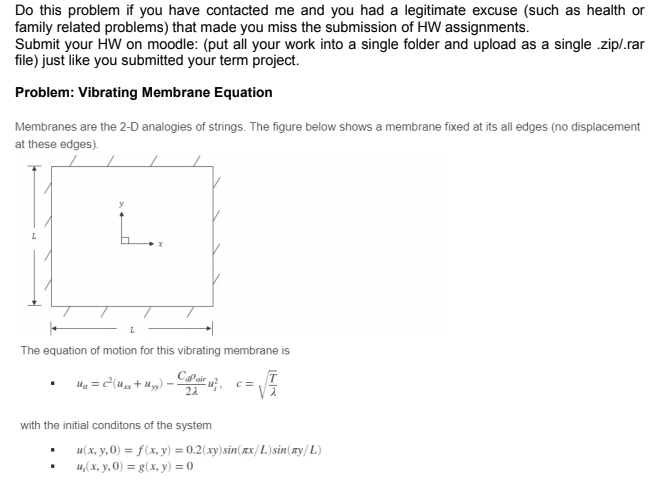
Do this problem if you have contacted me and you had a legitimate excuse (such as health or family related problems that made you miss the submission of HW assignments. Submit your HW on moodle: (put all your work into a single folder and upload as a single .zipl.rar file) just like you submitted your term project. Problem: Vibrating Membrane Equation Membranes are the 2-D analogies of strings. The figure below shows a membrane fixed at its all edges (no displacement at these edges). 2 L L L The equation of motion for this vibrating membrane is (+ y Capair 22 V with the initial conditons of the system u(x, y,0) = f(x,y) = 0.2( xy) sin(xx/L) sin(xy/L) u(x, y,0) = g(x, y) = 0 where L is the edge length of the membrane, u(x, y,t) is the displacement along the z axis, c is the wave speed, T is the force per unit length, 1 is the mass per unit area, C, is the drag coefficient of the membrane, and Pair is the air density The values for these parameters are given as follows: L = 1.5m T = 20N/m 1 = 100g/m2 C = 0.7 Pair = 1.225kg/m . To find the displacements u(x, y, t) at the interior points, the partial differential equation must be partitioned into grids with dx = dy = 0.05m and the time is increased with the step size dt = 0.002s. The displacement u at time dt is approximated with Taylor formula of order n = 2 as u(x, y, dt) = u(x, y,0) + u, (x, y,0)dt + " (x, y,0) dre 2! And the velocity u, is upgraded at all time steps as 4,(x, y, tl),(x, y, tk-1) + 4,(x, y, 1-1)dt The displacements u at times greater than dt must be approximated with the center-difference formulas of order och?). (Refer to your Course Book Ch. 6 Numerical Differentiation Formulas p. 339) In your script, please answer the following questions. (a) Find the initial acceleration of the center of the membrane (L/2, L/2,0). Assign it the variable named u_c. (b) Plot the displacement of the center of the membrane u . t) over (o 1] seconds. How does its vibrational behavior change over time? Why? (c) Animate the vibration of the membrane over the same time domain using the function drawnow. (When you upload your script to Grader, please comment the animation part because Grader does not animate the motion, and it takes time to show the final results. Later on, these animations will be uncommented on MATLAB to be evaluated by us.) Set the axis limits to x = [0,L), y = [0, L) and z = [-0.5,0.5] (d) Do you implement the Explicit or Implicit method? Why? Briefly explain it in a sentence. (e) If dt = 0.004, how does the model behave? Is it a good idea to increase the step size to make it less computational? Remark. Drag force is opposite the direction of the velocity. Use sign() function to take this into effect. Do this problem if you have contacted me and you had a legitimate excuse (such as health or family related problems that made you miss the submission of HW assignments. Submit your HW on moodle: (put all your work into a single folder and upload as a single .zipl.rar file) just like you submitted your term project. Problem: Vibrating Membrane Equation Membranes are the 2-D analogies of strings. The figure below shows a membrane fixed at its all edges (no displacement at these edges). 2 L L L The equation of motion for this vibrating membrane is (+ y Capair 22 V with the initial conditons of the system u(x, y,0) = f(x,y) = 0.2( xy) sin(xx/L) sin(xy/L) u(x, y,0) = g(x, y) = 0 where L is the edge length of the membrane, u(x, y,t) is the displacement along the z axis, c is the wave speed, T is the force per unit length, 1 is the mass per unit area, C, is the drag coefficient of the membrane, and Pair is the air density The values for these parameters are given as follows: L = 1.5m T = 20N/m 1 = 100g/m2 C = 0.7 Pair = 1.225kg/m . To find the displacements u(x, y, t) at the interior points, the partial differential equation must be partitioned into grids with dx = dy = 0.05m and the time is increased with the step size dt = 0.002s. The displacement u at time dt is approximated with Taylor formula of order n = 2 as u(x, y, dt) = u(x, y,0) + u, (x, y,0)dt + " (x, y,0) dre 2! And the velocity u, is upgraded at all time steps as 4,(x, y, tl),(x, y, tk-1) + 4,(x, y, 1-1)dt The displacements u at times greater than dt must be approximated with the center-difference formulas of order och?). (Refer to your Course Book Ch. 6 Numerical Differentiation Formulas p. 339) In your script, please answer the following questions. (a) Find the initial acceleration of the center of the membrane (L/2, L/2,0). Assign it the variable named u_c. (b) Plot the displacement of the center of the membrane u . t) over (o 1] seconds. How does its vibrational behavior change over time? Why? (c) Animate the vibration of the membrane over the same time domain using the function drawnow. (When you upload your script to Grader, please comment the animation part because Grader does not animate the motion, and it takes time to show the final results. Later on, these animations will be uncommented on MATLAB to be evaluated by us.) Set the axis limits to x = [0,L), y = [0, L) and z = [-0.5,0.5] (d) Do you implement the Explicit or Implicit method? Why? Briefly explain it in a sentence. (e) If dt = 0.004, how does the model behave? Is it a good idea to increase the step size to make it less computational? Remark. Drag force is opposite the direction of the velocity. Use sign() function to take this into effect