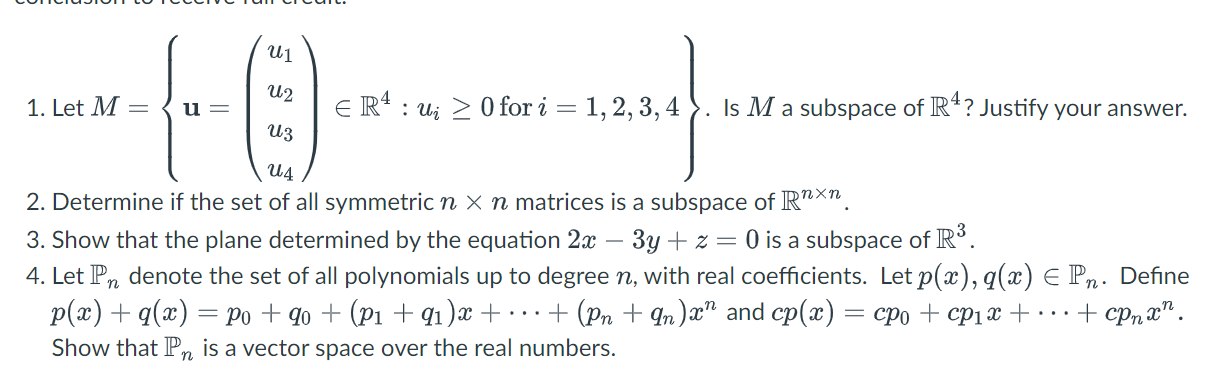
U1 U2 1. Let M = u = ER : ui _ 0 for i = 1, 2, 3, 4 Is M a subspace of IR$? Justify your answer. U3 U4 2. Determine if the set of all symmetric n X n matrices is a subspace of Rxn. 3. Show that the plane determined by the equation 2x - 3y + z = 0 is a subspace of 3. 4. Let Pn denote the set of all polynomials up to degree n, with real coefficients. Let p(a), q(a) E Pn. Define p(x) + q(x) = po + go + (p1 + q1)x+ ...+ (Pn + qn)2" and cp(a) = cpo + cpix + ... + cpman. Show that Pn is a vector space over the real numbers