Question: UBC: UBC WW09: Problem 23 (1 point) = Ka (x+6x+58) (****) (a) Find the interval of values for q with the property that (for

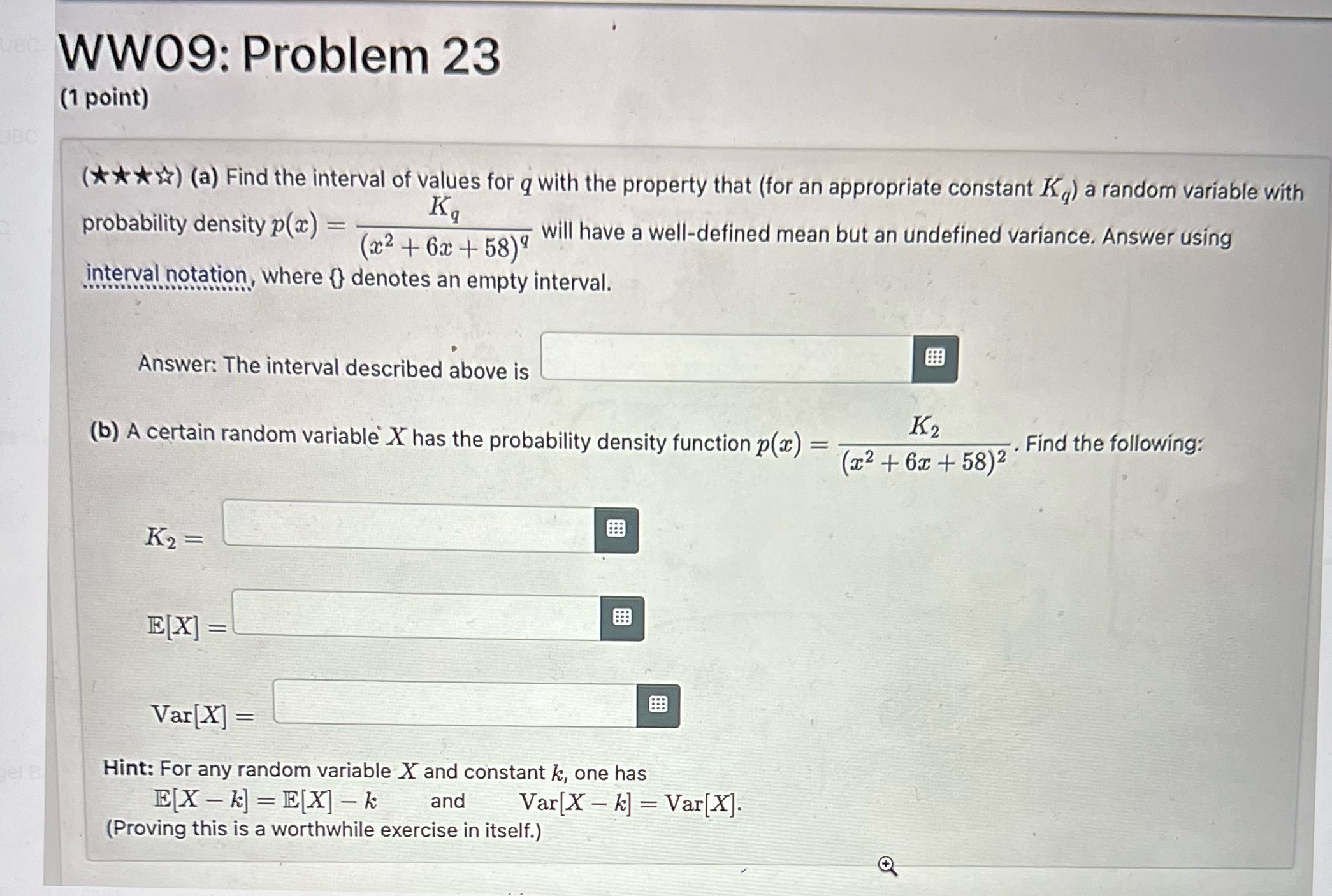
UBC: UBC WW09: Problem 23 (1 point) = Ka (x+6x+58) (****) (a) Find the interval of values for q with the property that (for an appropriate constant K) a random variable with probability density p(x) will have a well-defined mean but an undefined variance. Answer using interval notation, where {} denotes an empty interval. gel B Answer: The interval described above is (b) A certain random variable X has the probability density function p(x) = K2 (x+6x+58) . Find the following: K2= EX= Var[X] = Hint: For any random variable X and constant k, one has EX-k] EX-k and Var[X-k] = Var[X]. (Proving this is a worthwhile exercise in itself.)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Required information [The following information applies to the questions displayed below.] Information on Kwon Manufacturing's activities for its first month of operations follows: a. Purchased...

How are Australian Accounting regulators working to adopt this new standard? What challenges are they facing in this process

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

Digital Communication I X A B C D Y Hosts X and Y are communicating through the data network provided by the switches A, B, C and D and the links interconnecting them as shown above. Initially all...

Possible Multiple Choice Questions for the Exam. Focus on the topics discussed in class. Chapter 1 Multiple Choice Identify the choice that best completes the statement or answers the question. ____...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

U.S. Copyright Law (title 17 of U.S. code) governs the reproduction and redistribution of copyrighted material. Downloading this document for the purpose of redistribution is prohibited. Chapter 15...

nodes, but at least its bias can be quantified by Markov Chain L. INTRODUCTION analysis and thus can be corrected via appropriate re-weighting The popularity of online social networks (OSNs) in...

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

Instructor: Basu Dipanker Course: MAT-240-Q6622-16EW6 Assignment: 6-2 MyStatLab: Module Six Problem Set 1. Determine whether the scatter diagram indicates that a linear relation may exist between the...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

If the median of the distribution given below is 28.5, find the values of x and y. Class 0-10 10-20 20-30 30-40 40-50 50-60 Frequency 5 20 15 y 5 x Total 60

Last year, one division of Hagauer.com, a dot-com sports industry service fi rm that provides real-time analysis of mechanical stress due to athlete injury, had $250,000 in taxable income. This year,...

Whatisthedurationofafive-year,$1,000Treasurybondwitha10percentsemiannualcoupon sellingatpar?Sellingwithayieldtomaturityof12percent?14percent?Whatcanyouconclude about the relationship between duration...

Problem 4: [5 Marks] In the circuit shown in figure below, device A receives 4 kW at 0.6 pf lagging, device B receives 2 kVA at 0.5 pf leading, while device C is inductive and consumes 1 kW and...

Describe how the Internet of Things (IoT) technologies affect corporate data security interests in an environment in which much so-called white-collar work is being done from home due to COVID. Area...

For the circuit shown in the following figure below: i(t) 52 5 mF ww 50cos(200/+20 ) + 10 mH v(t) 32 42 a) Find i(t) and v(t). b) Determine the average power delivered to 50 and 30 resistors. c)...

Use nodal analysis to find V in the circuit of figure shown below. 202 402 www 120 15 V 6 Z30 A 30 2 soa

Design a minimum-mass symmetric three-bar truss (the area of member 1 and that of member 3 are the same) to support a load P, as was shown in Fig. 2.9. The following notation may be used: Pu = P cos...

2. Felicia is extremely insecure and lacks a clear sense of identity. She often clings to new friends and then hates them a month later. She has an intense fear of abandonment and rejection. Felicias...

=+a) As their sample size increases, whats the expected shape of the distribution of amounts purchased in the sample?

=+6. In 2008 and 2009, Systemax bought two failing electronics stores, Circuit City and CompUSA. They have Exercises M11_SHAR8696_03_SE_C11.indd 386 14/07/14 7:30 AM Exercises 387 kept both the names...