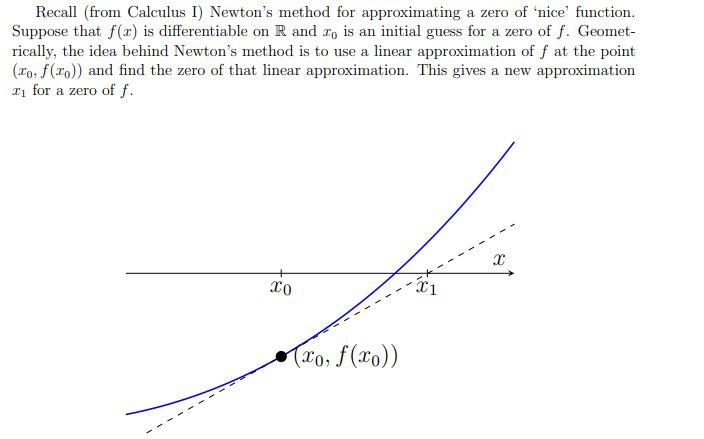
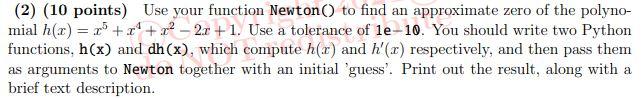
Under suitable conditions, I will usually be a better approximation than to, and this process can be repeated until an approximation of desired accuracy is achieved (or until it becomes obvious that the produced sequence is diverging). Working out the resulting formulas gives a sequence of successive approximations determined by In+1 = In Clearly, this is invalid if f'(In) = 0, and on a computer we actually need to be concerned with f'(In) being too close to zero. (1) (10 points) Write a function Newton (Function, Derivative, xo, epsilon), which implements Newton's method. The parameters to this function are as follows: Function: The name of a Python function which takes a single floating point number x and returns f(c), for some function f to be determined later. Derivative : As above, except this function evaluates and returns the derivative f'(x) of the same function. tion. above, ex redan evaluates x : An initial point for Newton's method. epsilon: A tolerance; the function should return the first number In in the sequence for which \f(In)