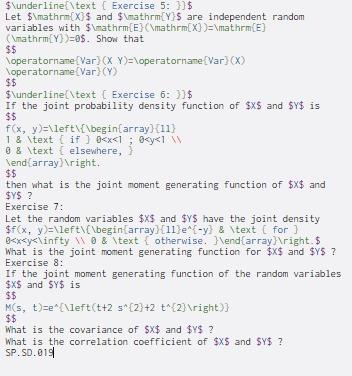
$\underline{\text Exercise 5: })$ Let $\mathrm{X}$ and $\mathrm{Y}$ are independent random variables with $\mathrm{E}\mathrm{X])=\mathrm{E} (\mathrm{Y})=05. Show that $$ operatorname Var) (XY)=\operatorname Var}(X) \operatornate Var}(Y) $$ $\underline[\text Exercise 6: 33$ If the joint probability density function of $X$ and $y$ is $$ f(x, y)=\left\{\begin{array}{11} 1 & \text { if ) 0