UndirectedGraph class $($do NOT use an existing Graph class, you must write your own!$)$

Undirected graphs can be stored in a data structure called an adjacency matrix, where a non$-$zero value

stored at row x and column y in the matrix means there exists an edge connecting vertices x and y$.$

Note that when storing an undirected graph in a matrix, you can either:

$*$ Make sure that both $($row x$,$ column y$)$ and $($row y$,$ column x$)$ are always set to the same value, or:

$*$ Use only half the matrix, the "upper triangle," by ensuring that the column number y is always

greater than or equal to the row number x when storing a value for an edge connecting x and y$.$

You may use either approach when storing the graph. For example, in a graph with five vertices, both of

these matrices store the same graph:

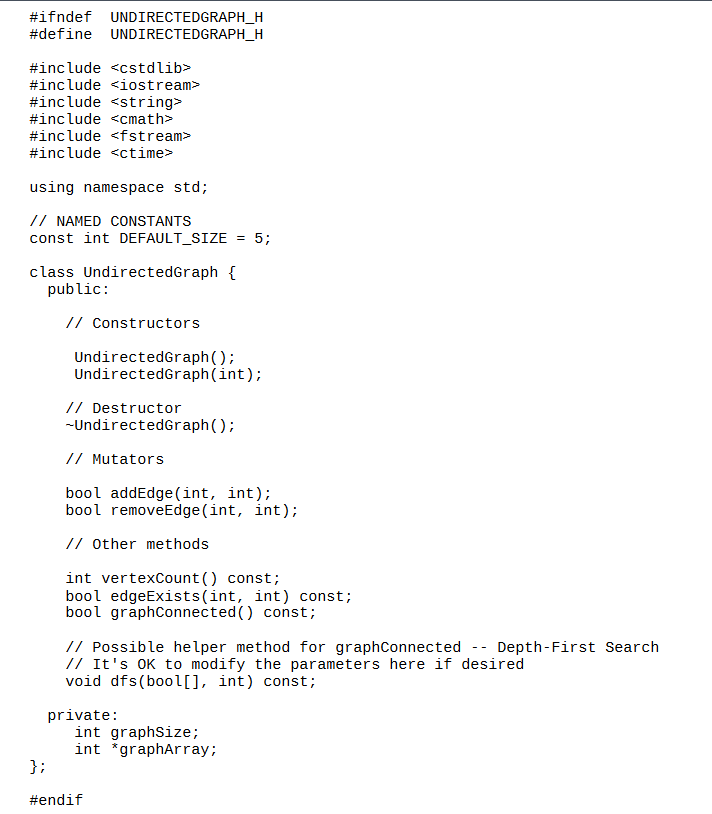
First, write methods appropriate to support an UndirectedGraph class:

$-$ Constructors to create an edgeless graph with a given number of vertices passed as an argument. Set a

default number of vertices for a zero$-$argument constructor. Each constructor will dynamically allocate the

array or vector the contains the matrix. NOTE that dynamic allocation of $2-$D arrays isn't something that

C$++$ supports! If using arrarys, consider using a "flat" single$-$dimensional array, and use a formula to

convert an edge from vertex i to vertex j on a graph with v vertices $($where i and j range from $0$ to v$-1)$ to

map to array$[$i$*$v $+$ j$]$ in a one$-$dimensional array. If using an upper$-$triangle approach to store edges, just

make sure that j $>=$ i when performing the calculation. There'll be "wasted" space in the array, but that's of

no concern here.

$-$ An accessor method int vertexCount$()$ that returns the number of vertices in the graph.

$-$ A method bool edgeExists$($int$,$ int$)$ that returns true if an edge exists between the two specified vertex

numbers.

Cal Poly Humboldt $-$ CS $211$ Fall $2024-$ Assignment #$4$ p$.2$ of $2$

$-$ You are not required to allow users to change the number of vertices once the graph is created.

$-$ bool addEdge$($int$,$ int$)$ and bool removeEdge$($int$,$ int$)$ methods for adding and removing edges from the

graph. An edge is defined by the two vertices it connects, so each method should expect two int values,

each representing a vertex. Each method should return true if the action was performed and false if it

wasn't $($for example, the edge already exists, or there was no edge to be removed$).$ Your addEdge method

should also check to make sure you are NOT adding a "loop" edge that connects a vertex to itself!

$-$ A method bool graphConnected$()$ that does the following:

$*$ Allocates a a bool array of size equal to the number of vertices, used to indicate whether a vertex

has been "marked" during traversal. Initialize all values to false.

$*$ Starting from any vertex, performs a "walk" using the edges, marking visited vertices along the way.

A recursive search $($using a helper function$)$ is best here, but be sure to pay attention to which

vertices have already been visited when doing your recursion so you don't infinitely recurse!

$*$ Check your marked$-$vertex array, and return true if all vertices were marked during the search $($i$.$e$.,$

the graph is connected$),$ and false otherwise.

There are several ways to determine whether a graph is connected $($that is$,$ whether it's possible to get

from any vertex to any other vertex via a path$).$ You can consult the text for possible methods.

Here is a description of a method for determining connectivity, from the Wikipedia page on "Connectivity

$($graph theory$)",$ with some minor edits:

$*$ Begin at any arbitrary vertex in the graph, and "mark" it$.($You can use the bool array or

vector of size $|$ V $|,$ the number of vertices in the graph, to record vertices are being

marked.$)$

$*$ Proceed from that vertex using the edges in either a depth$-$first or a breadth$-$first search,

marking all vertices reached. $($Marking can be useful so that you know which vertices you've

already visited to avoid excessive recursion, or even infinite recursion!$)$

$*$ Once the graph has been traversed, if all vertices are marked, then the graph is connected.