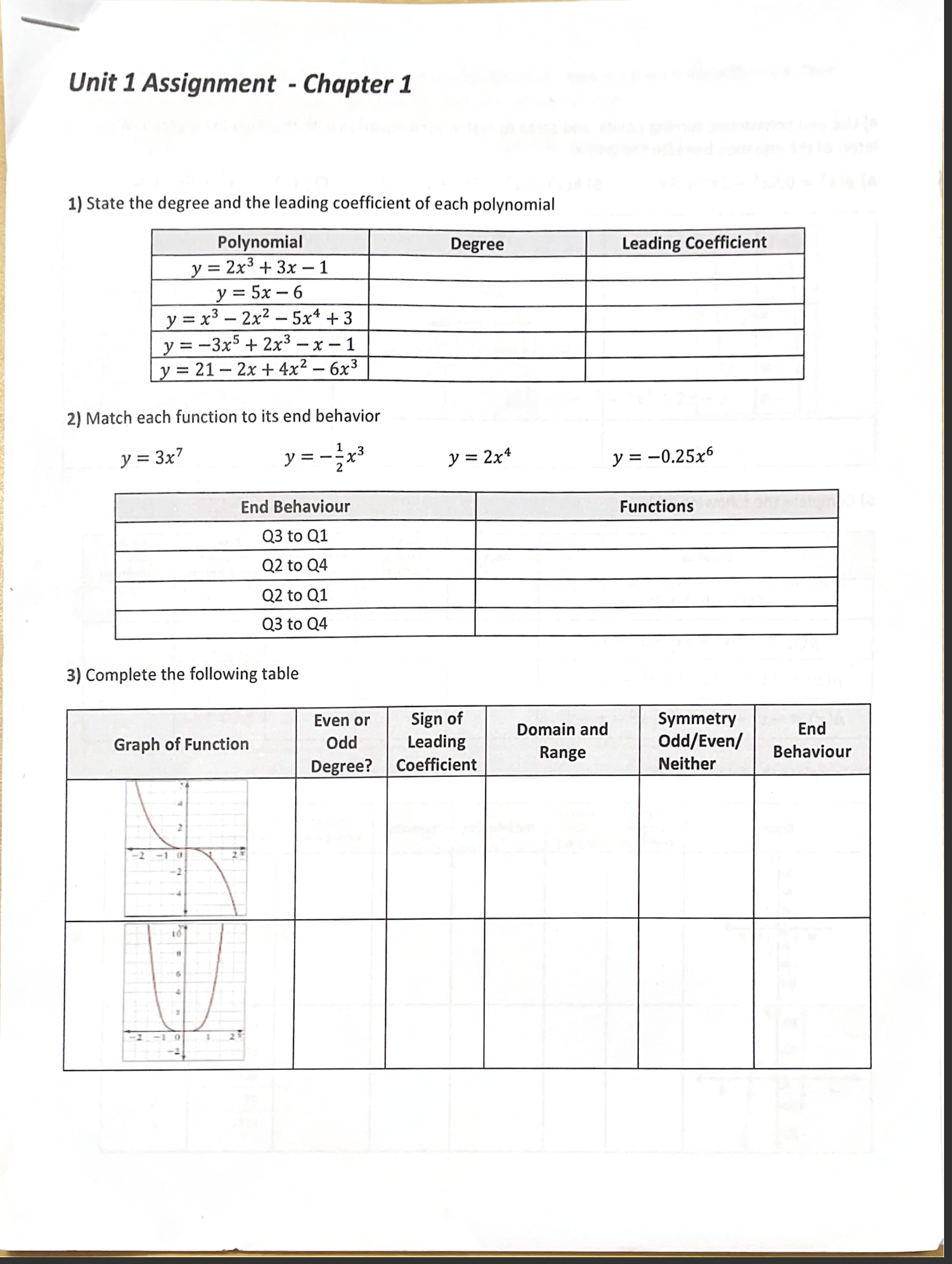
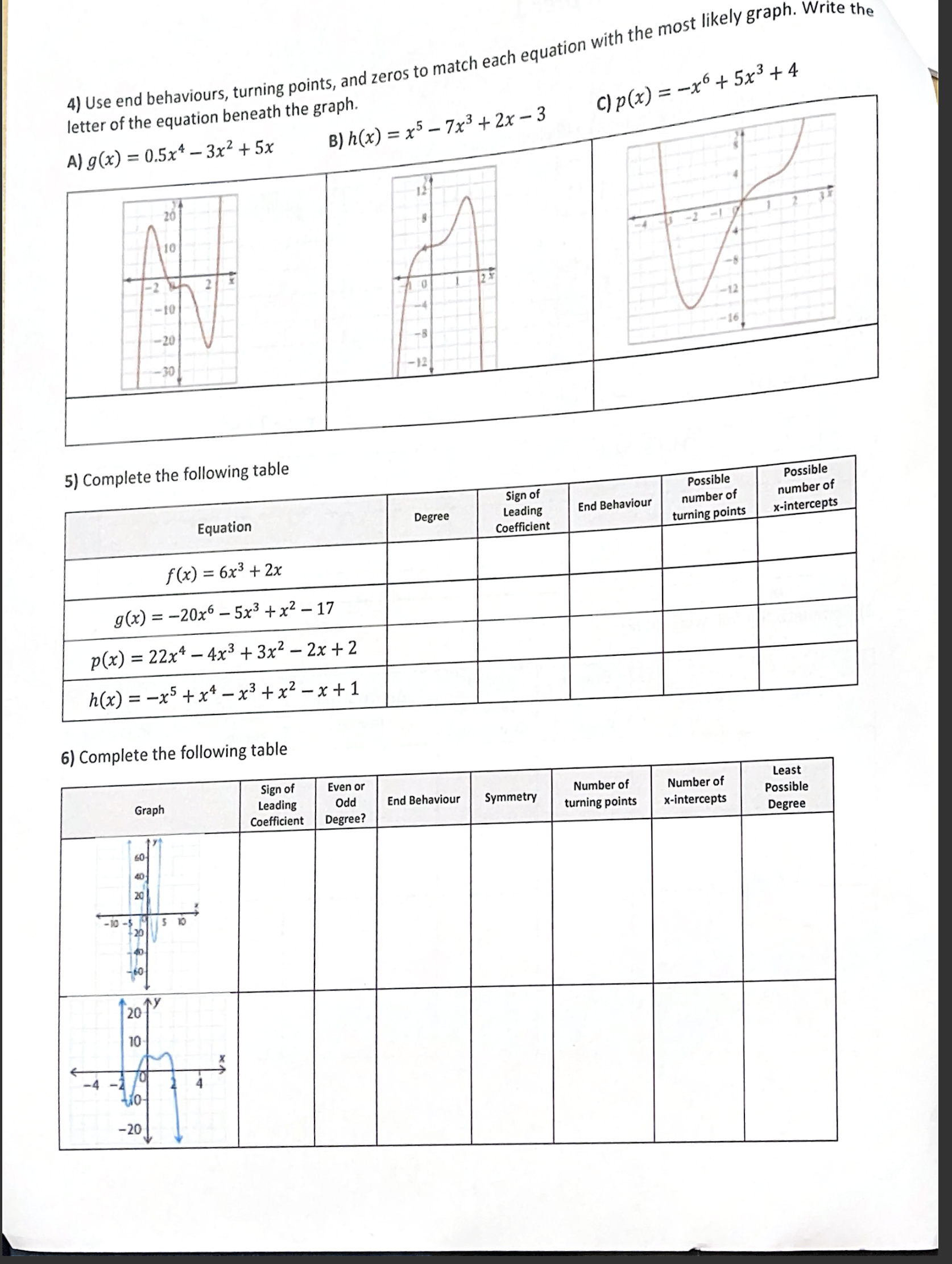
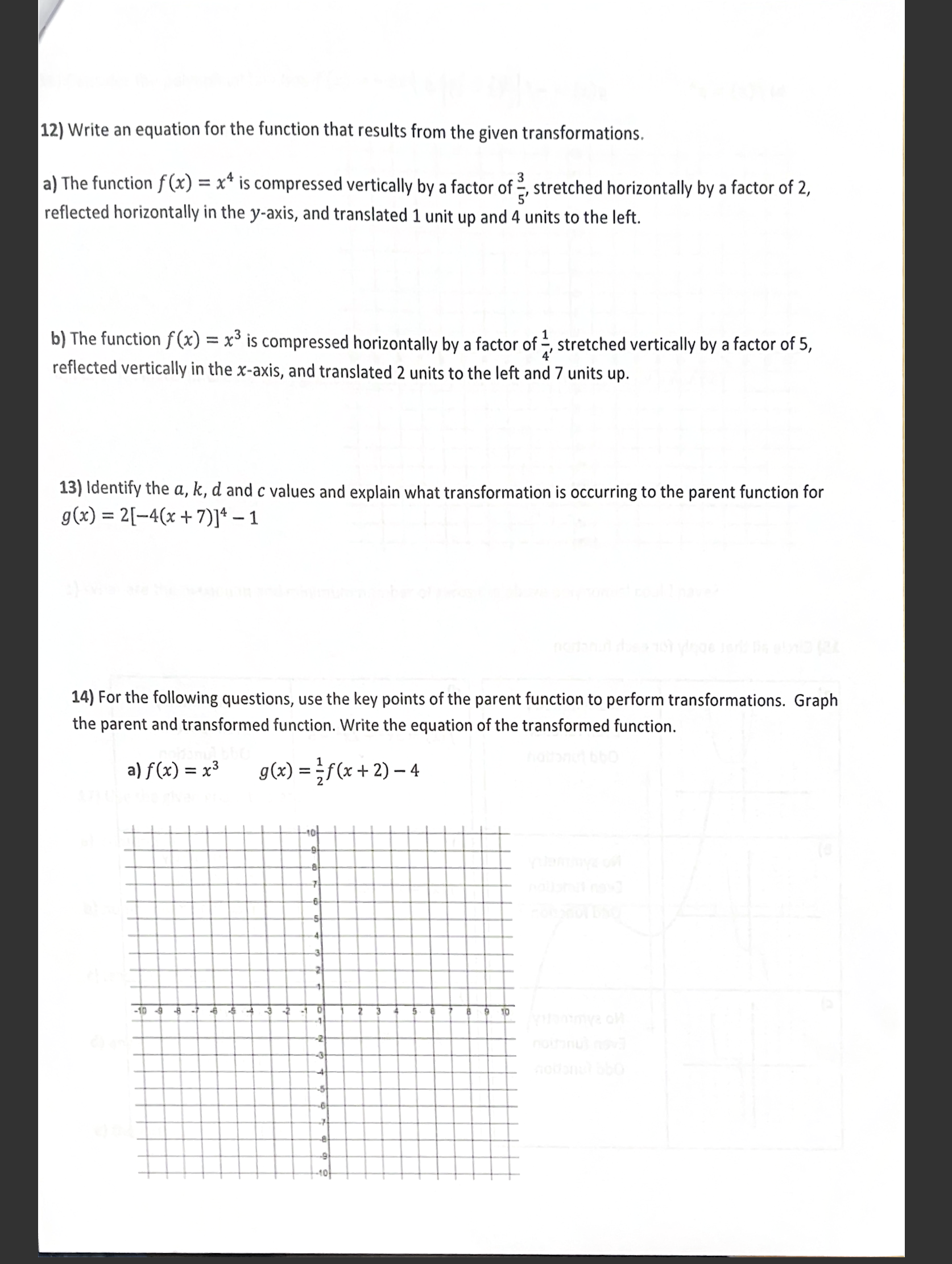
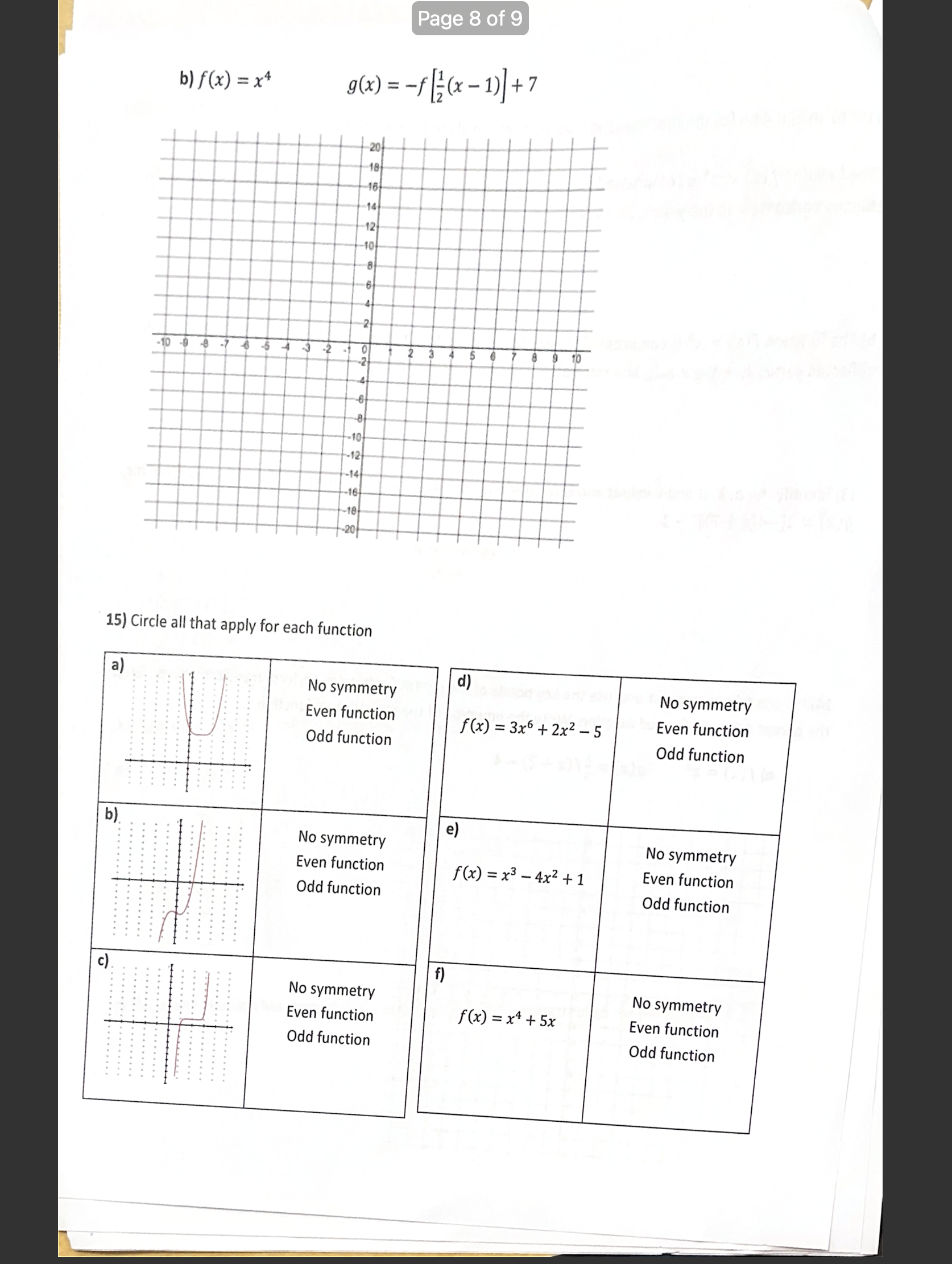
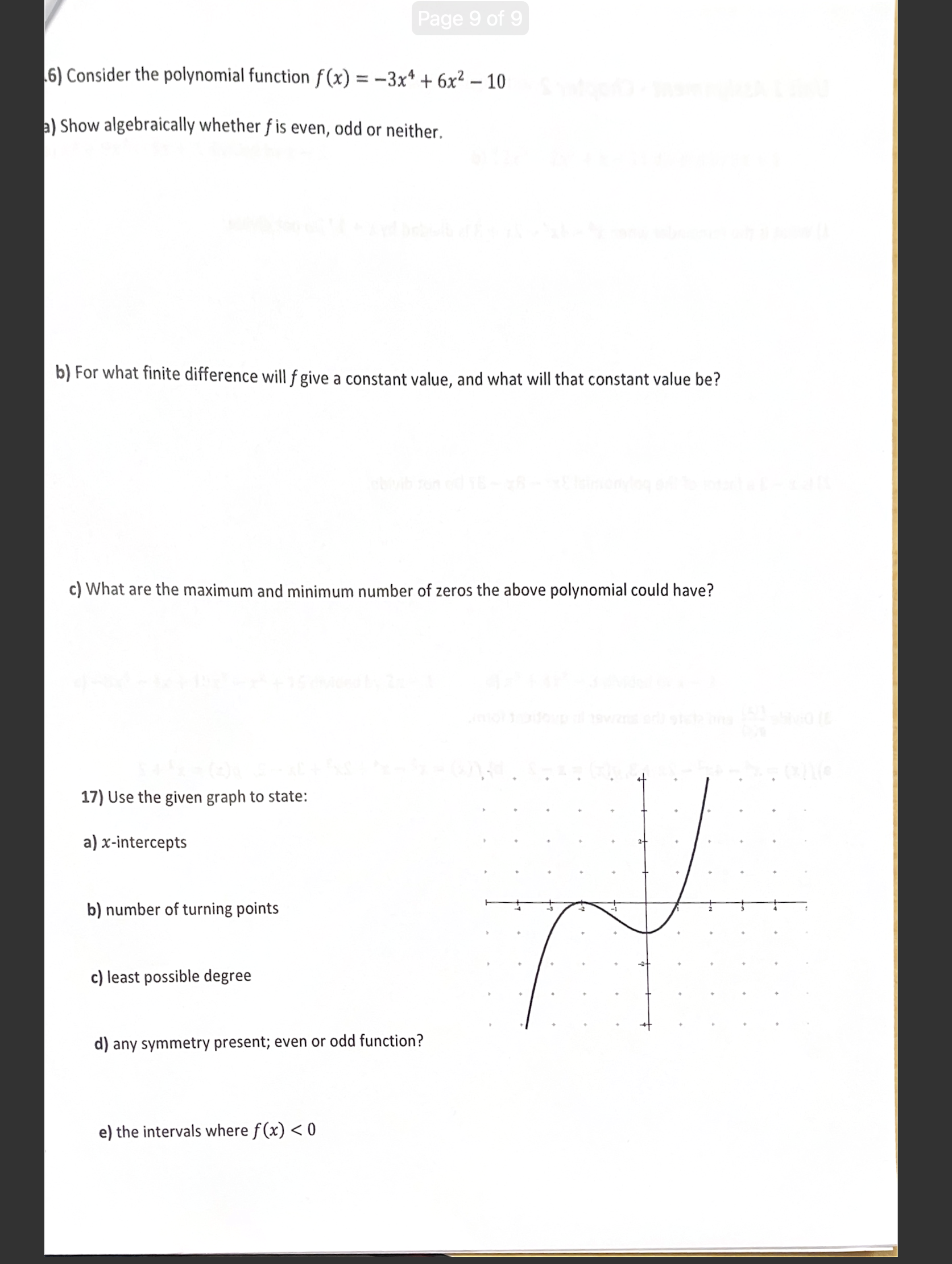
\\ Unit 1 Assignment - Chapter 1 1) State the degree and the leading coefficient of each polynomial Even or Symmetry Domain and Oodd Leading 0dd/Even/ Range Degree? | Coefficient Neither t likely graph. Write the : he mos yation W! h 4) Use end behaviours, turning points, and zeros 10 match eached beneath the graph. | p(x) . 5+ 5x3 L4 letter of the equation 7% + 23 0.5x*3x*+5% B) h(x) = x5 - A) g(x) possible number of possible number of sign of Degree Leading End Behaviour Coefficient turning points Sign of Evenor Leading odd Least Coefficient Possible Degree 7) State the degree of the polynomial function that corresponds to each constant finite difference. Then determine the value of the leading coefficient for each polynomial function. a) fifth differences = -60 b) third differences = 42 8) For each function, find the value of the constant finite differences. a) g(x) = 0.5x* 3x% + 5x b) h(x) = x = 7x3 + 2x - 3 9) Use finite differences to determine the degree and value of the leading coefficient for each polynomial function. a) X y -3 124 d 4 -1 8 0 i 1 -4 2 -31 3 104 4 2a7 b) X y 2 -229 1 =5 0 3 1 -7 2 -53 3 -128 4 35 5 1213 10) For each function, complete the chart and sketch a possible graph of the function labelling key points. a) f(x) = (x+1)(x -3)(x+2) y-intercept Leading Coefficient End Behaviour x-intercepts Degree b) g(x) = - x(x + 1) (x + 2)2 Degree Leading Coefficient End Behaviour x-intercepts y-intercept\f11) For each graph, state... i) the least possible degree and the sign of the leading coefficient | ii) the x-intercepts (specify order of zero) and the factors of the function iiii) the intervals where the function is positiveegative a) ' i) degree: \\ ' leading coefficient: i) x-intercepts: factors: b) ol i) degree: leading coefficient: | i) x-intercepts: factors: 12) Write the equation of each of the following functions: a) T b) The quartic function has zeros at -3, -1, and 2 (order 2) and passes through the point (1, 4) 12) Write an equation for the function that results from the given transformations. a) The function f(x) = x* is compressed vertically by a factor of % stretched horizontally by a factor of 2, reflected horizontally in the y-axis, and translated 1 unit up and 4 units to the left. b) The function f(x) = x* is compressed horizontally by a factor of %, stretched vertically by a factor of 5, reflected vertically in the x-axis, and translated 2 units to the left and 7 units up. 13) \\dentify the a, k, d and values and explain what transformation is occurring to the parent function for g(x) =2[-4(x + 7)])* -1 14) For the following questions, use the key points of the parent function to perform transformations. Graph the parent and transformed function. Write the equation of the transformed function. Af)=x* g =3fx+2)-4 Page 8 of 9 b ) f (x ) = x4 g(x) = -f =(x - 1) +7 - 10 15) Circle all that apply for each function a) d) No symmetry No symmetry Even function f (x) =3x6 +2x2 -5 Even function Odd function Odd function b) e) No symmetry No symmetry Even function f(x) = x3 -4x2 + 1 Even function Odd function Odd function c) f ) . . . . No symmetry No symmetry Even function f(x) = x4+5x Even function Odd function Odd function . . . . . . . ..Page 9 of 9 6) Consider the polynomial function f (x) = -3x4 + 6x2 - 10 a) Show algebraically whether f is even, odd or neither. b) For what finite difference will f give a constant value, and what will that constant value be? c) What are the maximum and minimum number of zeros the above polynomial could have? 17) Use the given graph to state: a) x-intercepts b) number of turning points c) least possible degree d) any symmetry present; even or odd function? e) the intervals where f (x)