Unit Commitment Problem in Power Generation Planning

This problem involves optimizing power generation while minimizing costs, using Linear Programming $($LP$).$

Step $1$: Define Decision Variables

xi$,$t: Number of generators of type i running at time t$.$

pi$,$t: Total power produced by type i at time t$.$

ui$,$t: Binary variable $(1$ if generator i starts at time t$,0$ otherwise$).$

Step $2$: Define Constraints

Meet Demand $+15\%$ Reserve:

$$pi$,$t$1\mathrm{.}15$demand$$at$$time$$t$\backslash$sum pi$,$t $\backslash$geq $1\mathrm{.}15\backslash$times $\backslash$text$\{$demand at time $\}$ t$$pi$,$t$1\mathrm{.}15$demand$$at$$time$$t

Ensures demand and reserve capacity are met.

Generator Capacity Limits:

xi$,$t$$Pmin,i$$pi$,$t$$xi$,$t$$Pmax,ixi,t $\backslash$times P$\_\{\backslash$text$\{$min$\},$i$\}\backslash$leq pi$,$t $\backslash$leq xi$,$t $\backslash$times P$\_\{\backslash$text$\{$max$\},$i$\}$xi$,$t$$Pmin,i$$pi$,$t$$xi$,$t$$Pmax,i$$

Ensures generators operate within safe limits$.$

Startup Constraints:

xi$,$t$$xi$,$t$1$ui$,$txi,t $-$ xi$,$t$-1\backslash$leq ui$,$txi,t$$xi$,$t$1$ui$,$t

Tracks startup costs when generators start running.

Total Generators Available:

$$xi$,$t$$Total$$available$$generators$$of$$type$$i$\backslash$sum xi$,$t $\backslash$leq $\backslash$text$\{$Total available generators of type $\}$ i$$xi$,$t$$Total$$available$$generators$$of$$type$$i

Step $3$: Objective Function

Minimize total cost:

Total$$Cost$=$t$$i$[$xi$,$t$$Cmin$,$i$+($pi$,$t$$xi$,$t$$Pmin$,$i$)$Cextra$,$i$+$ui$,$t$$Cstartup$,$i$]\backslash$text$\{$Total Cost$\}=\backslash$sum$\_\{$t$\}\backslash$sum$\_\{$i$\}[$xi$,$t $\backslash$cdot C$\_\{\backslash$text$\{$min$\},$i$\}+($pi$,$t $-$ xi$,$t $\backslash$cdot P$\_\{\backslash$text$\{$min$\},$i$\})\backslash$cdot C$\_\{\backslash$text$\{$extra$\},$i$\}+$ ui$,$t $\backslash$cdot C$\_\{\backslash$text$\{$startup$\},$i$\}]$Total$$Cost$=$t$$i$[$xi$,$t$$Cmin$,$i$+($pi$,$t$$xi$,$t$$Pmin$,$i$)$Cextra$,$i$+$ui$,$t$$Cstartup$,$i$]$

Components:

Fixed running costs at minimum level.

Costs for power above the minimum.

Startup costs.

Step $4$: Implement in Excel

Input Table:

List generator types, capacities, and cost parameters.Include hourly demand values.

Decision Variables $($Orange$)$:

xi$,$t: Number of generators running.pi$,$t: Power output.ui$,$t: Binary startup indicator.

Formulas $($Green$)$:

Enforce demand, generator limits$,$ and startup tracking.

Objective Function $($Yellow$)$:

Enter the cost formula for minimization.

Solver Setup:

Objective: Minimize total cost.Variables: xi$,$t$,$ pi$,$t$,$ ui$,$t$.$Constraints: Demand, generator limits$,$ startup tracking, and integer$/$binary restrictions.

Step $5$: Report Results

Mathematical model explanation.

Excel model structure $($color$-$coded cells: input data, decision variables, constraints, and costs$).$

Solver setup and solution explanation.

Summary of results:

Number of generators used per hour.Power output per generator type.Total generation cost.Cost savings if the $15\%$ reserve is removed.

Final Insight: Removing $15\%$ Reserve

Reduces the need for extra generators.

Cuts startup and running costs.

Highlights cost differences with and without the reserve.

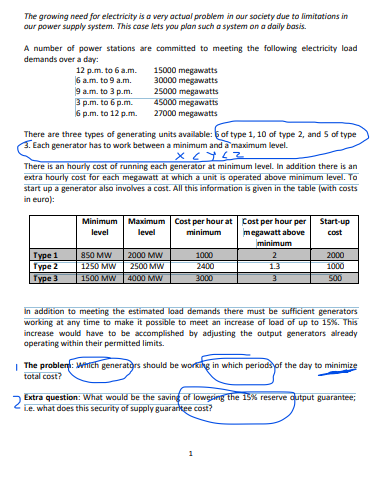
can you follow these instructions and make an excel sheet showing how should I do it and send me a screenshot regarding this assignment $?$