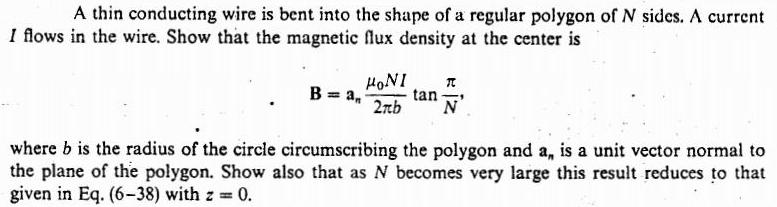
A thin conducting wire is bent into the shape of a regular polygon of N sides. A current I flows in the wire. Show that the magnetic flux density at the center is B = a, HONI 2nb tan where b is the radius of the circle circumscribing the polygon and a, is a unit vector normal to the plane of the polygon. Show also that as N becomes very large this result reduces to that given in Eq. (6-38) with z 0.