URGENT! (Java):

Use the following code to generate all of the possible districtings for the appropriate size of grid. A 5x5 should generate 1038 possibilities. A 6x6 will generate 53498 unique maps, and may take more than 10 minutes to find them all, depending on your code. You need not bother with maps of 7x7 or larger for this assignment. After generating all of the unique district maps, sort them according to compactness measures. The maps with the smallest total perimeter should come first; if two maps are tied on total perimeter, break the tie using lowest average skew measure. If the two are still tied, use the average Isoperimetric measure. If they are still tied, use the average Square Reock measure to break the tie.

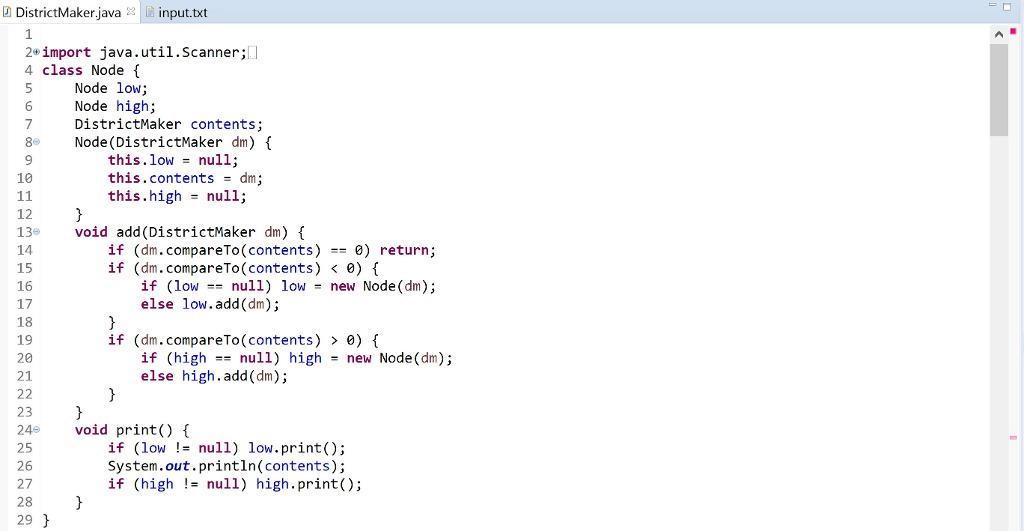
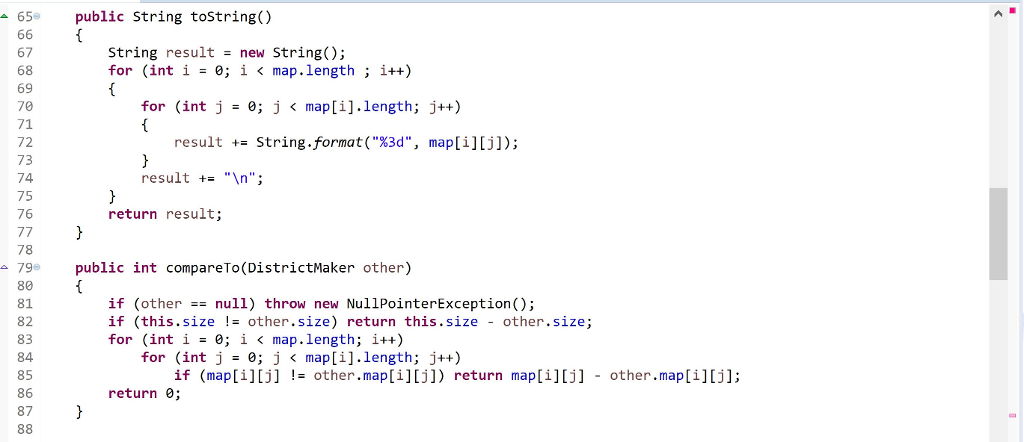
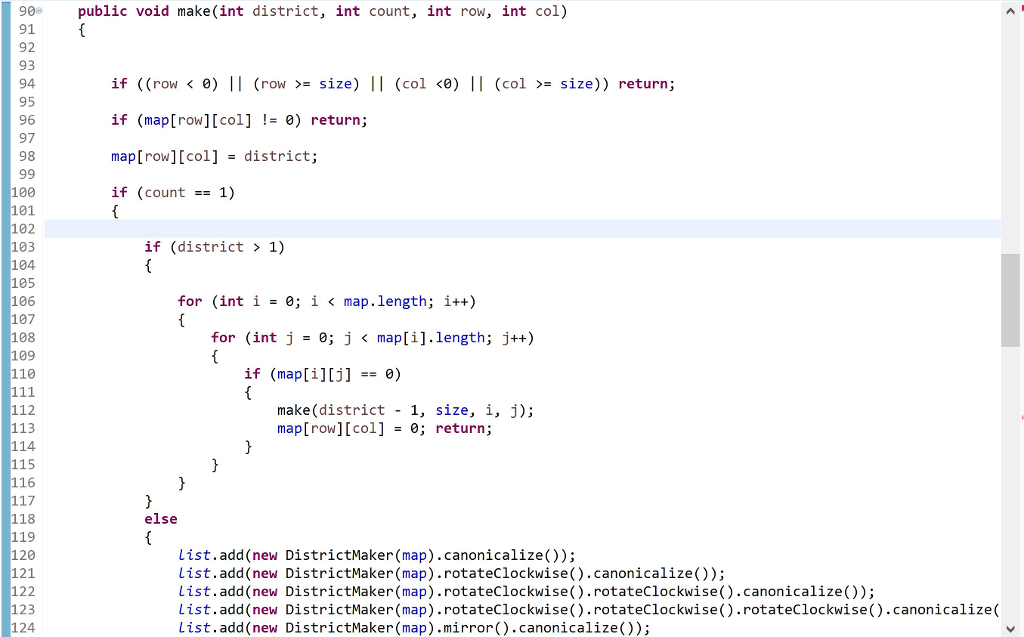
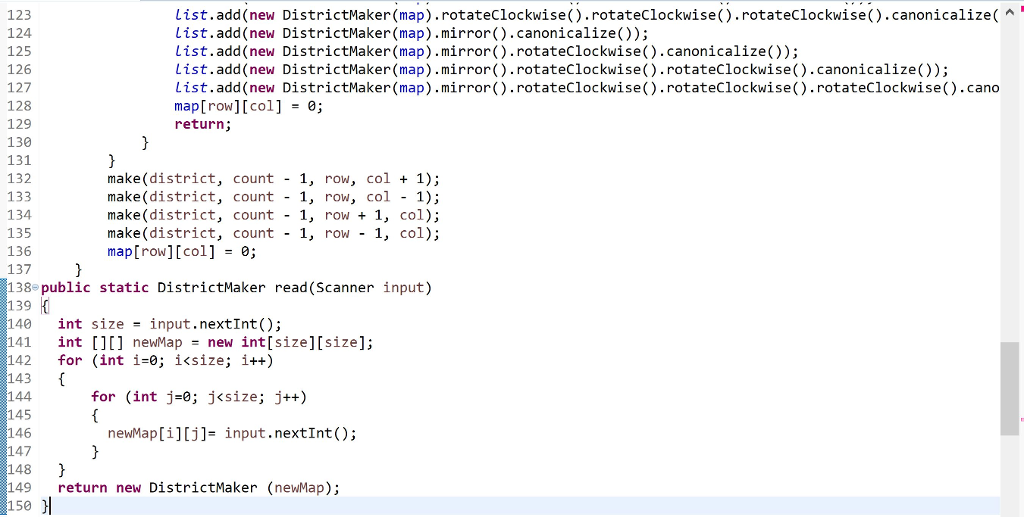
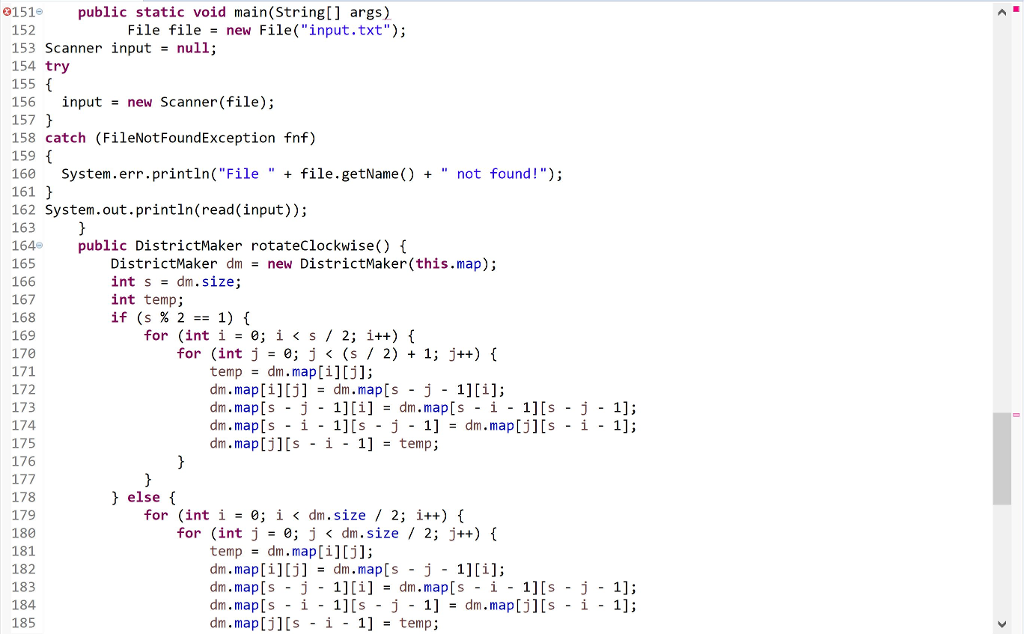
Finally, starting with the most "compact" districtings first, calculate which party would carry the vote in each of the randomized voting scenarios for each map. This work is embarrassingly parallel -- the domain can be safely decomposed trivially among the threads. If one exists, print out the first compact districting that reliably skews the vote to the minority party on the map.

Input to your Gerrymander class will look like this 1000000 simulations 18 threads 5 districts 0.600 0.18 0.400 8.10 .300 0.1 e.700 0.18 .200 8.10 0.123 .18 0.345 0.10 0.567 0.10 e.821 0.10 0.310 8.10 0.197 0.10 0.012 ?.10 0.746 0.10 0.468 0.10 0.276 0.10 The first line specifies that there will 1000000 simulations per district map. The second line specifies that 10 concurrent threads should be spawned to speed up the simulations. (Use load balancing, as discussed in Chapter 6.) The third line indicates that there will be five districts in the map. For simplicity, always assume that the grid is square, and the number of rows and columns is equal to the number of districts. The next five lines consist of 25 pairs of floating point numbers. The first value in each pair is an average percentage of the vote for the part of interest in a given square on the grid. 0.0 means no votes for the party of interest, 1-0 means 100% of the votes. The second value in each pair is a standard deviation. We will use the Java Random class to generate a normal distribution of values around the expected average for each of the voting simulations. To be more specific, the formula for generating the polling result for a specific cell in a particular simulation is that cell's average, plus the standard deviation multiplied by the next value from the Random.nextGaussian() method. In this way, we will simulate the uncertainty inherent in real elections Input to your Gerrymander class will look like this 1000000 simulations 18 threads 5 districts 0.600 0.18 0.400 8.10 .300 0.1 e.700 0.18 .200 8.10 0.123 .18 0.345 0.10 0.567 0.10 e.821 0.10 0.310 8.10 0.197 0.10 0.012 ?.10 0.746 0.10 0.468 0.10 0.276 0.10 The first line specifies that there will 1000000 simulations per district map. The second line specifies that 10 concurrent threads should be spawned to speed up the simulations. (Use load balancing, as discussed in Chapter 6.) The third line indicates that there will be five districts in the map. For simplicity, always assume that the grid is square, and the number of rows and columns is equal to the number of districts. The next five lines consist of 25 pairs of floating point numbers. The first value in each pair is an average percentage of the vote for the part of interest in a given square on the grid. 0.0 means no votes for the party of interest, 1-0 means 100% of the votes. The second value in each pair is a standard deviation. We will use the Java Random class to generate a normal distribution of values around the expected average for each of the voting simulations. To be more specific, the formula for generating the polling result for a specific cell in a particular simulation is that cell's average, plus the standard deviation multiplied by the next value from the Random.nextGaussian() method. In this way, we will simulate the uncertainty inherent in real elections