Use a numerical example to illustrate how National determines the optimal length-of-rent control.

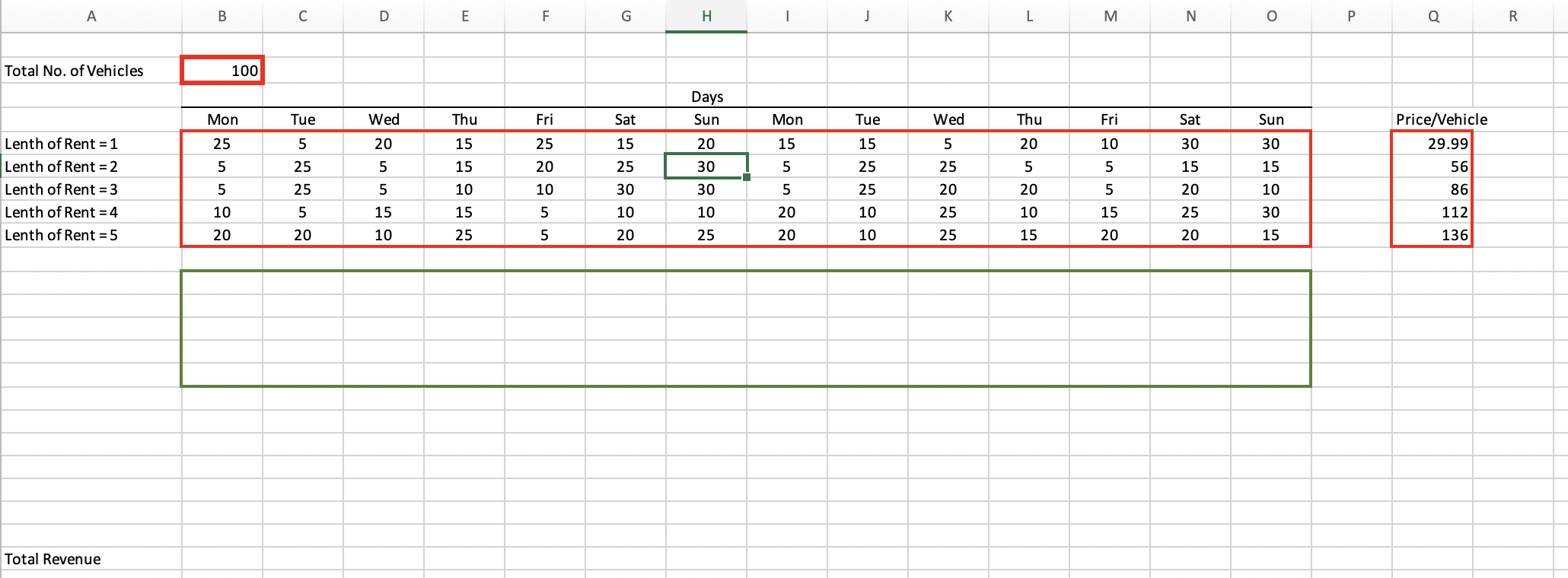
NATIONAL CAR RENTAL ganization. It has supported more flexible fleet strategies and tactics. It has led in the development and implementation of new products (Saturday-night keep rates, pre- paid rates, guaranteed rates). It has helped National to give customers a higher level of service, especially our late-booking corpo- rate clients. It has upheld our ability to serve customers who suffer broken reservations by our competitors. But most important, in its first year of coast-to-coast deployment, the operational revenue management de- partment allowed the creation and realiza- tion of $56 million in incremental revenue. APPENDIX: Length-of-Rent Control Reservations are accepted or rejected based on length-of-rent controls. Optimal length-of-rent controls are determined by a revised simplex algorithm with upper bounds for the following formulation: maximize N L rijXijr i=1 j-1 subject to i L Skjxkj = Ci k=max(1,i-L) j=1 1 if k + j>i Skj 0 otherwise Xij Hij where N = the number of arrival days in the planning horizon, L = the number of length-of-rent catego- ries, i = {i: 1,..., N) arrival days within the planning horizon, k = {k: 1,..., N) arrival days that impact day i availability, j= (j: 1,..., L) length-of-rent categories, x = the decision variable for arrival day i and length-of-rent category j, Hij = mean remaining demand for length- of-rent category j, C = remaining capacity for arrival day i, and rij = expected revenue for length-of-rent category j on arrival day i. The LP solution is degraded to maximum and minimum length-of-rent recommenda- tions by a voting scheme that weights the LOR recommendations for each arrival day according to its proximity to a future con- strained day. Planned Upgrades The planned upgrades algorithm is based on a heuristic that was developed for allo- cating airline reservations inventory on a single flight leg (see Belobaba [1989]). This EMSR (expected marginal seat revenue) heuristic computes protection levels for each booking class. A protection level is the number of cars that should be reserved for the demand in the current class. The opti- mality conditions for a constrained revenue maximization problem are as follows: dR dR d; d =Xij, where R is the revenue function, A represents the expected marginal revenue of the last car allocated to each class, and j is the protection level for class j. Once the EMSR heuristic determines pro- tection levels for each class, the planned- upgrades algorithm determines the avail- ability in each class. The availability number that appears on the reservations system is the sum of the availability for fu- ture bookings and the current bookings for the car class. Availability for car classes with excess demand is computed as the fleet in that class plus any cars available from higher classes to cover the excess de- mand. The availability for car classes with excess fleet is computed as the fleet less A Total No. of Vehicles Lenth of Rent = 1 Lenth of Rent = 2 Lenth of Rent = 3 Lenth of Rent = 4 Lenth of Rent = 5 Total Revenue B 100 Mon 25 5 5 10 20 C Tue 5 25 25 5 20 D Wed 20 5 5 15 10 E Thu 15 15 10 15 25 F Fri 25 20 10 5 5 G Sat 15 25 30 10 20 H Days Sun 20 30 30 10 25 | Mon 15 5 5 20 20 J Tue 15 25 25 10 10 K Wed 5 25 20 25 25 L Thu 20 5 20 10 15 M Fri 10 5 5 15 20 N Sat 30 15 20 25 20 O Sun 30 15 10 30 15 P Q Price/Vehicle 29.99 56 86 112 136 R NATIONAL CAR RENTAL ganization. It has supported more flexible fleet strategies and tactics. It has led in the development and implementation of new products (Saturday-night keep rates, pre- paid rates, guaranteed rates). It has helped National to give customers a higher level of service, especially our late-booking corpo- rate clients. It has upheld our ability to serve customers who suffer broken reservations by our competitors. But most important, in its first year of coast-to-coast deployment, the operational revenue management de- partment allowed the creation and realiza- tion of $56 million in incremental revenue. APPENDIX: Length-of-Rent Control Reservations are accepted or rejected based on length-of-rent controls. Optimal length-of-rent controls are determined by a revised simplex algorithm with upper bounds for the following formulation: maximize N L rijXijr i=1 j-1 subject to i L Skjxkj = Ci k=max(1,i-L) j=1 1 if k + j>i Skj 0 otherwise Xij Hij where N = the number of arrival days in the planning horizon, L = the number of length-of-rent catego- ries, i = {i: 1,..., N) arrival days within the planning horizon, k = {k: 1,..., N) arrival days that impact day i availability, j= (j: 1,..., L) length-of-rent categories, x = the decision variable for arrival day i and length-of-rent category j, Hij = mean remaining demand for length- of-rent category j, C = remaining capacity for arrival day i, and rij = expected revenue for length-of-rent category j on arrival day i. The LP solution is degraded to maximum and minimum length-of-rent recommenda- tions by a voting scheme that weights the LOR recommendations for each arrival day according to its proximity to a future con- strained day. Planned Upgrades The planned upgrades algorithm is based on a heuristic that was developed for allo- cating airline reservations inventory on a single flight leg (see Belobaba [1989]). This EMSR (expected marginal seat revenue) heuristic computes protection levels for each booking class. A protection level is the number of cars that should be reserved for the demand in the current class. The opti- mality conditions for a constrained revenue maximization problem are as follows: dR dR d; d =Xij, where R is the revenue function, A represents the expected marginal revenue of the last car allocated to each class, and j is the protection level for class j. Once the EMSR heuristic determines pro- tection levels for each class, the planned- upgrades algorithm determines the avail- ability in each class. The availability number that appears on the reservations system is the sum of the availability for fu- ture bookings and the current bookings for the car class. Availability for car classes with excess demand is computed as the fleet in that class plus any cars available from higher classes to cover the excess de- mand. The availability for car classes with excess fleet is computed as the fleet less A Total No. of Vehicles Lenth of Rent = 1 Lenth of Rent = 2 Lenth of Rent = 3 Lenth of Rent = 4 Lenth of Rent = 5 Total Revenue B 100 Mon 25 5 5 10 20 C Tue 5 25 25 5 20 D Wed 20 5 5 15 10 E Thu 15 15 10 15 25 F Fri 25 20 10 5 5 G Sat 15 25 30 10 20 H Days Sun 20 30 30 10 25 | Mon 15 5 5 20 20 J Tue 15 25 25 10 10 K Wed 5 25 20 25 25 L Thu 20 5 20 10 15 M Fri 10 5 5 15 20 N Sat 30 15 20 25 20 O Sun 30 15 10 30 15 P Q Price/Vehicle 29.99 56 86 112 136 R