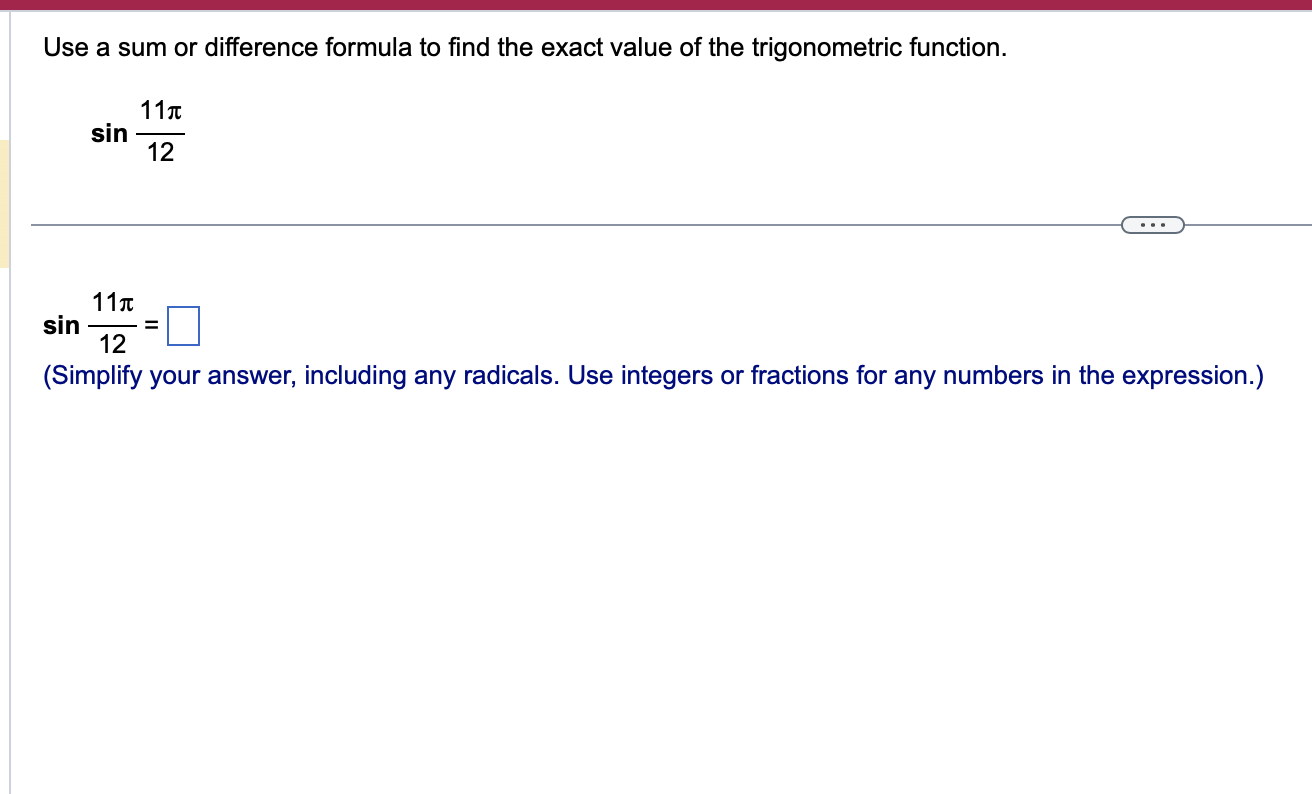
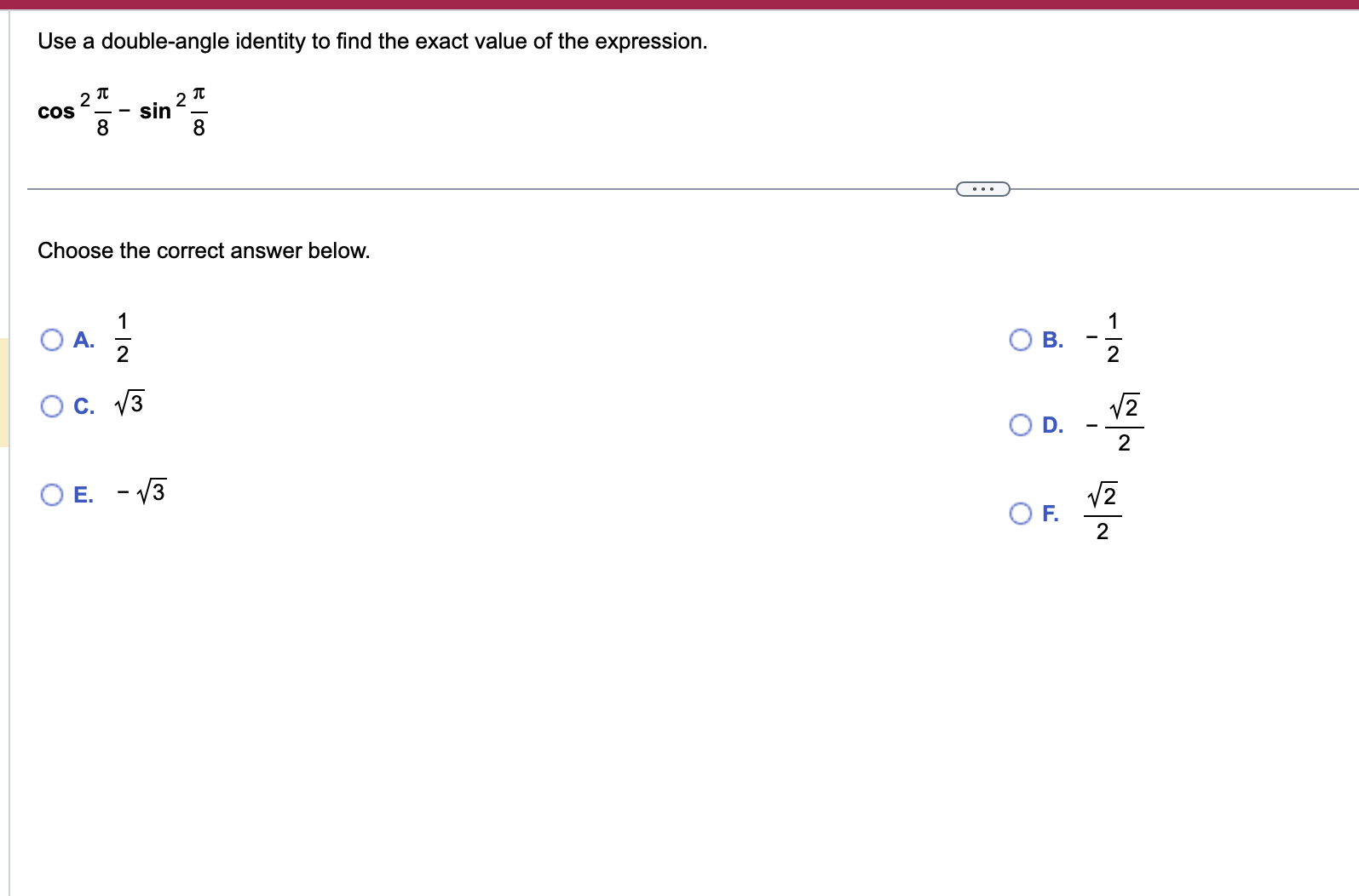
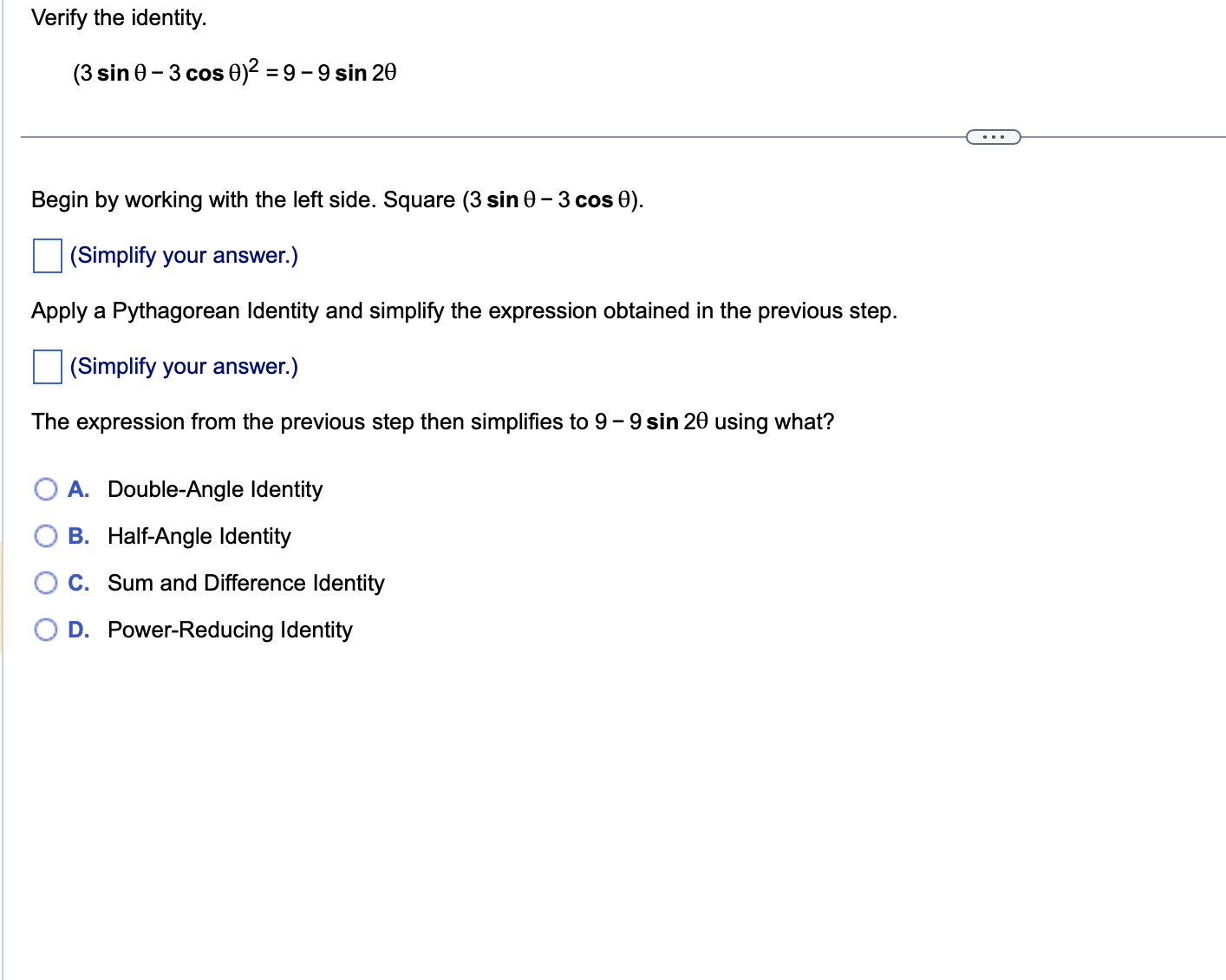
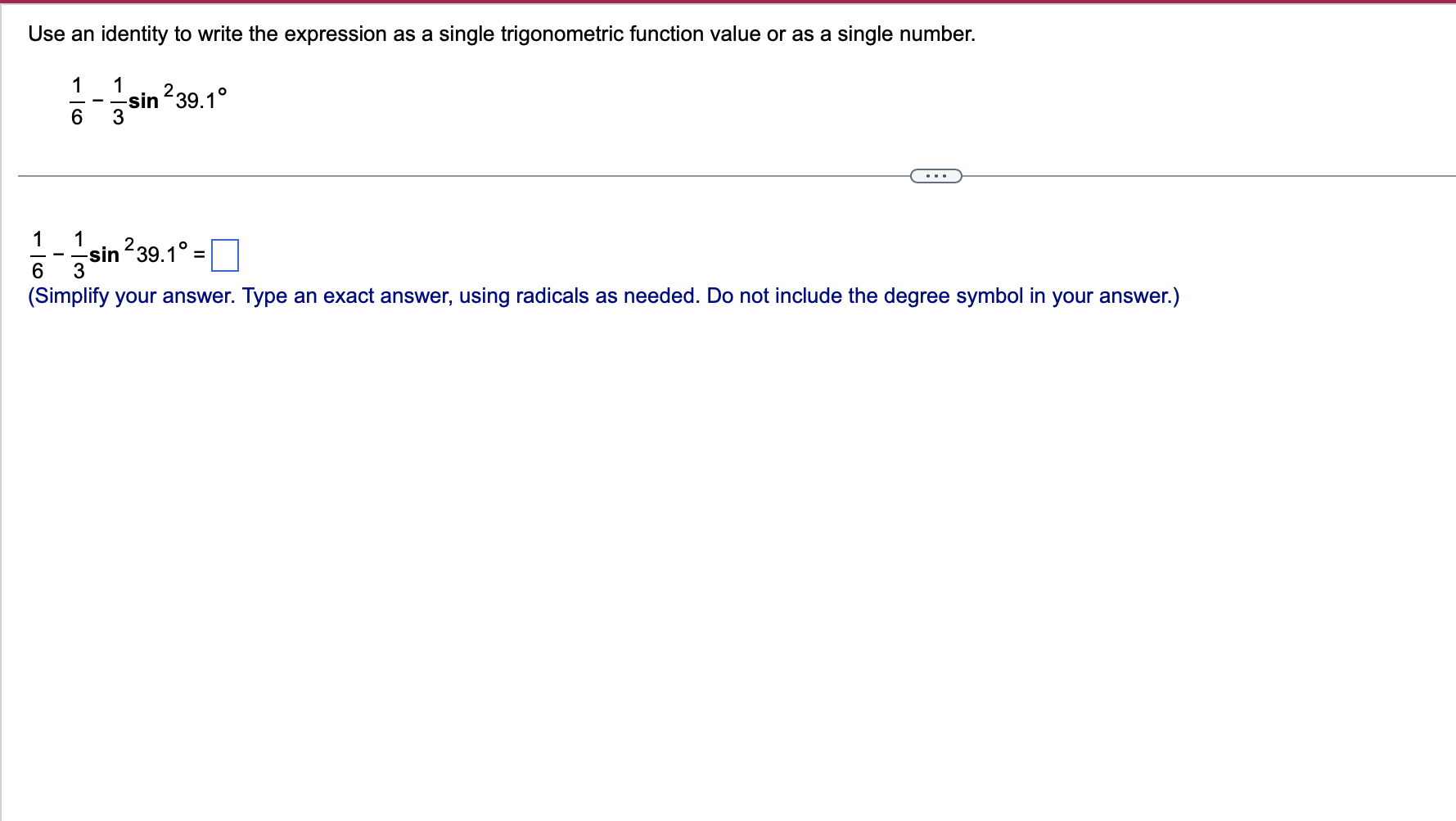
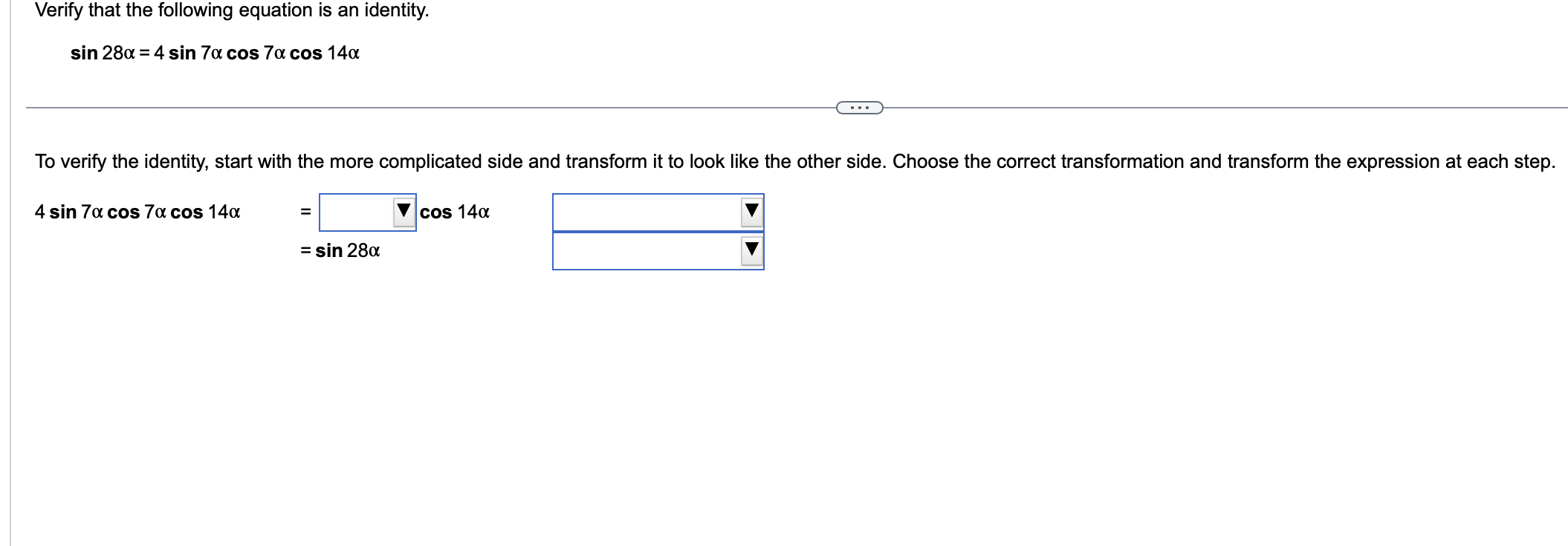
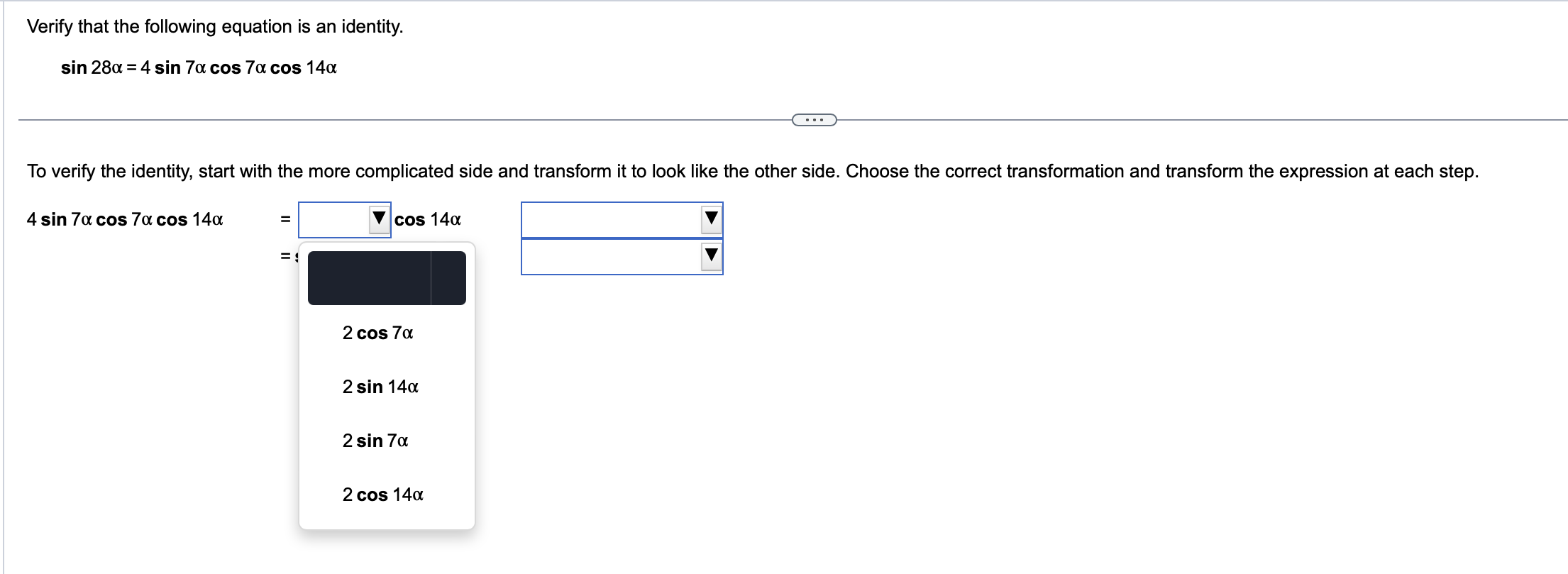
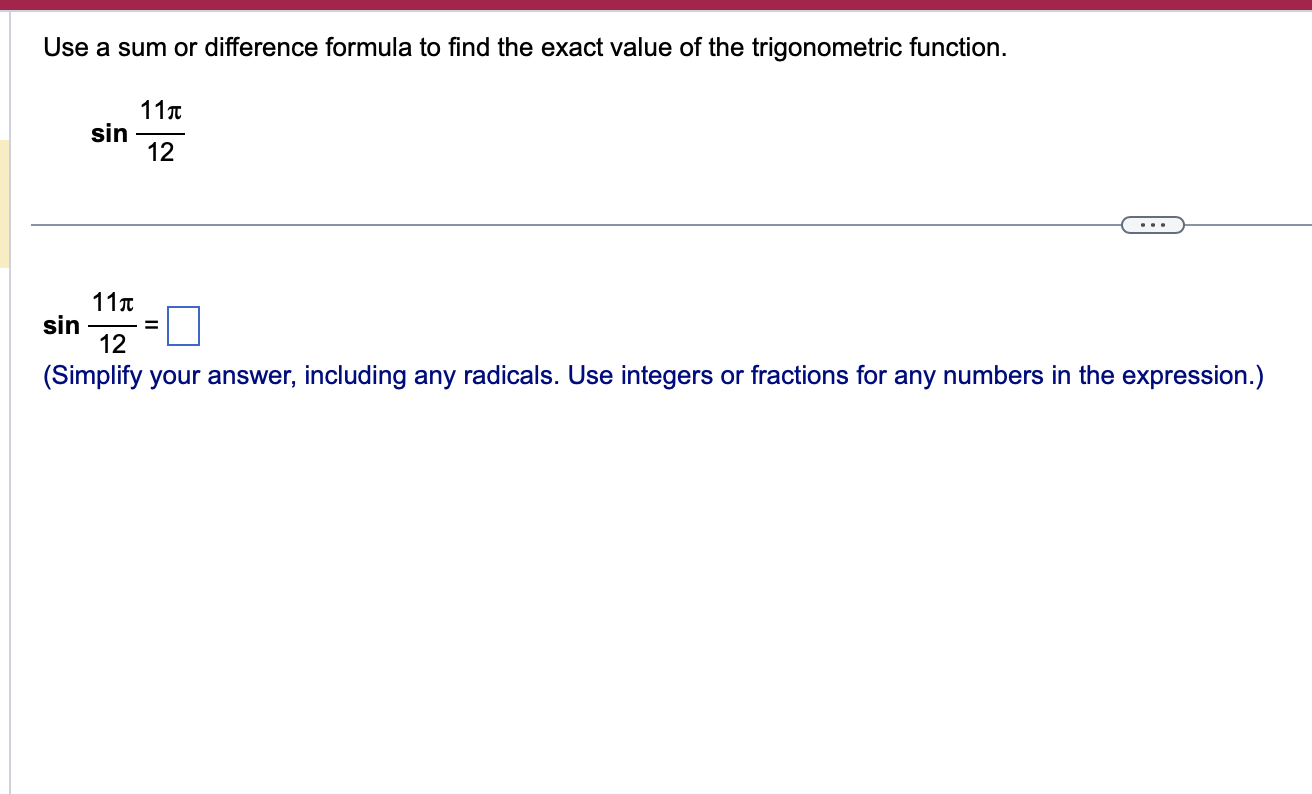
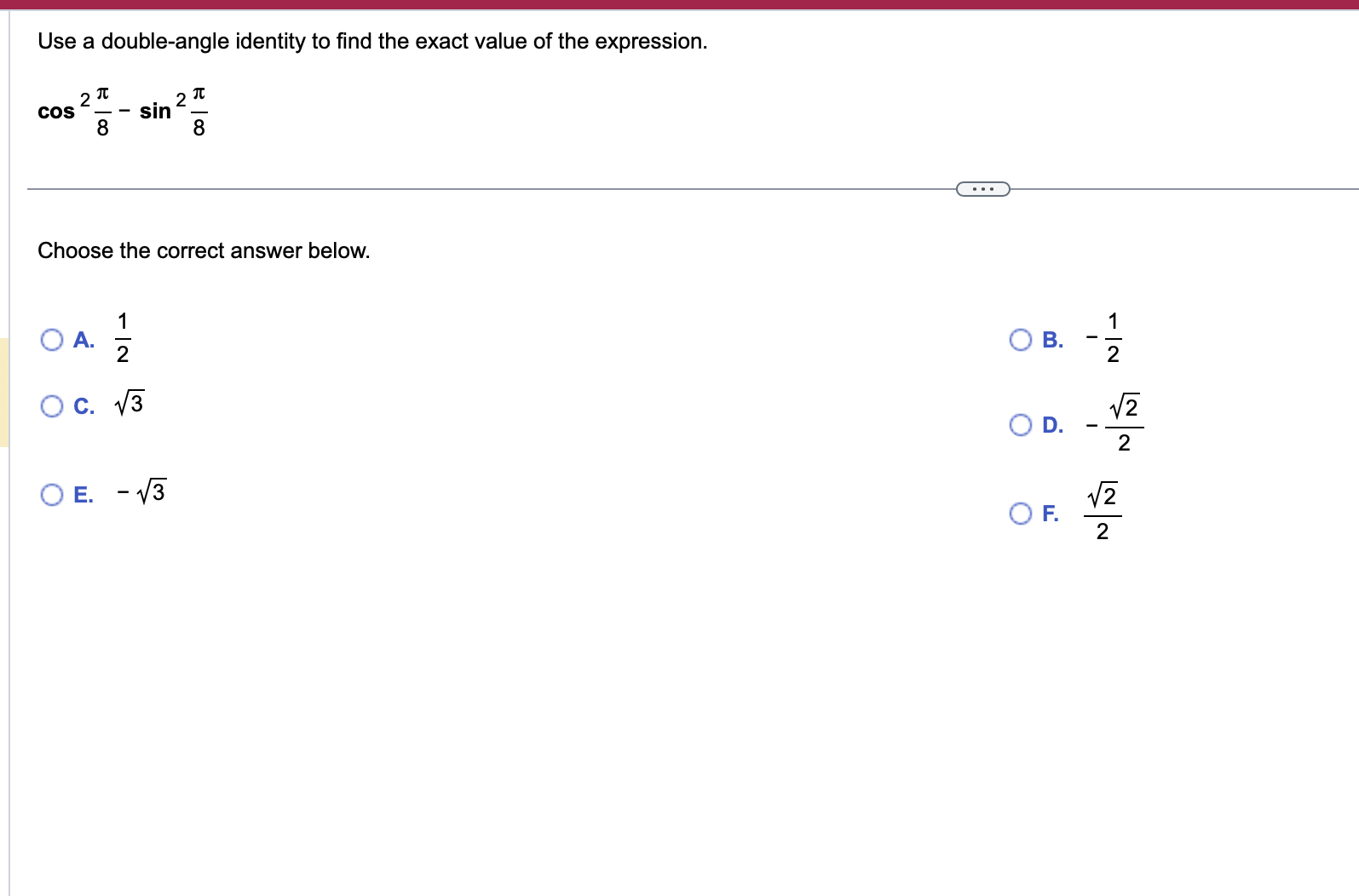
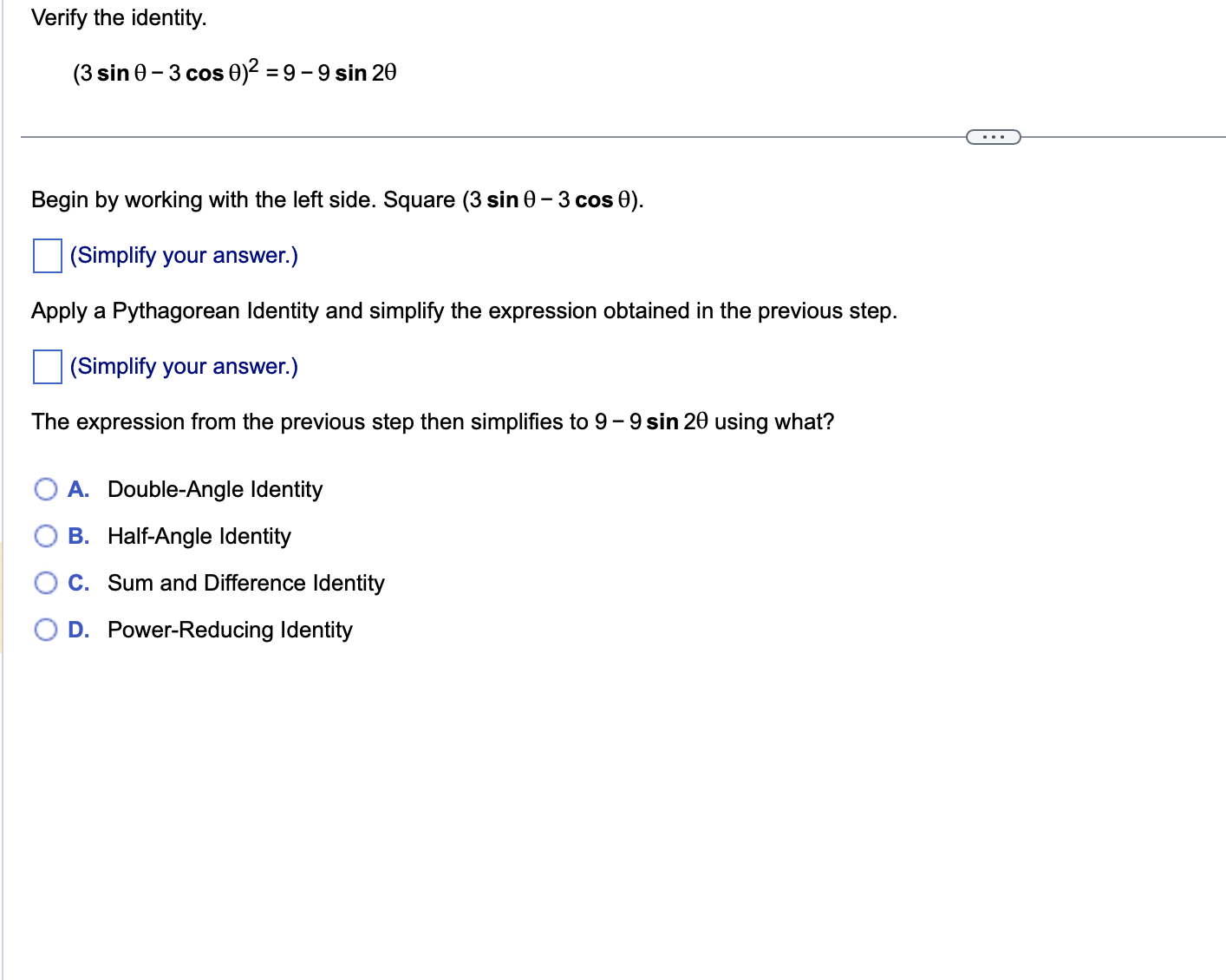
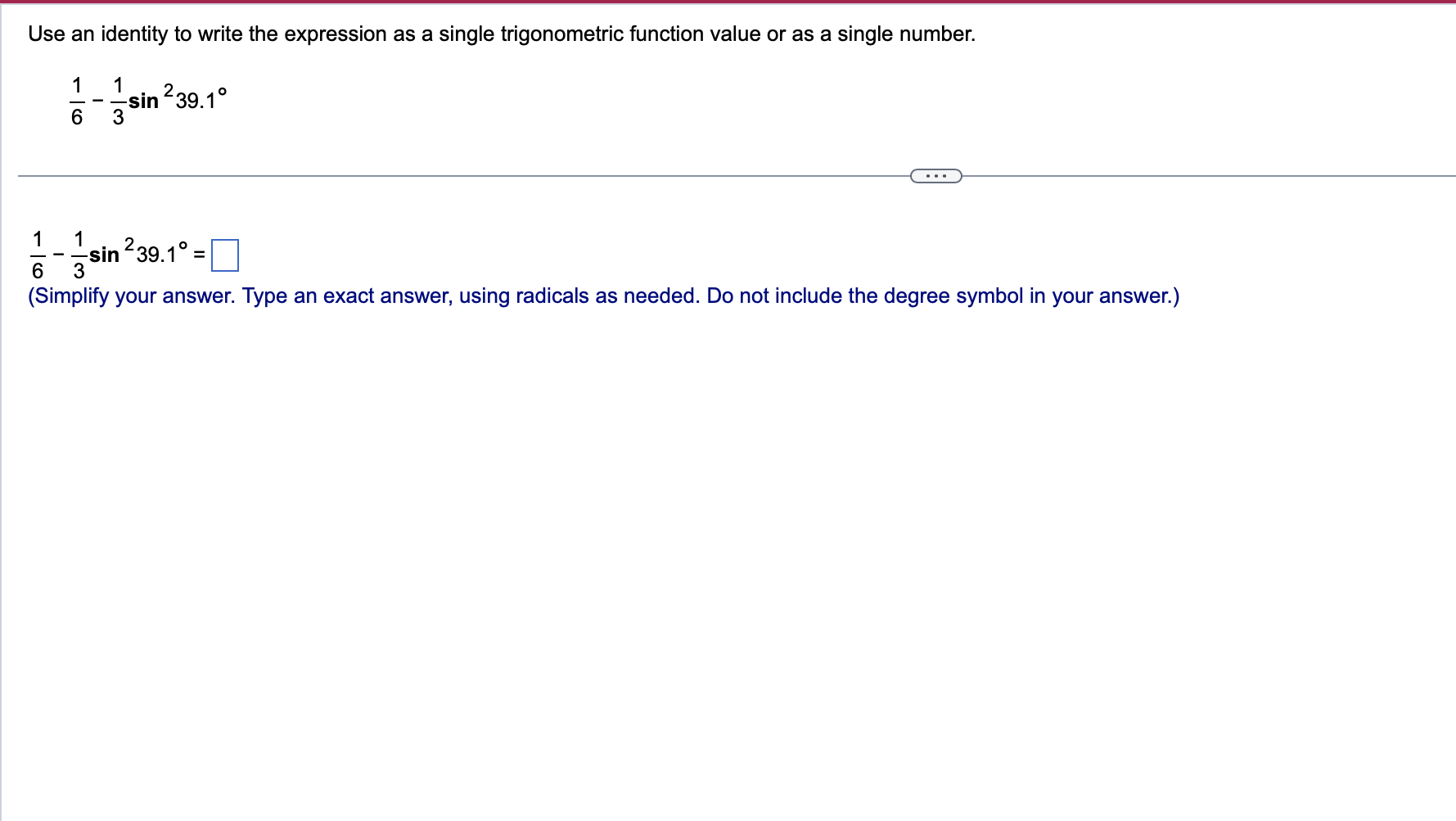
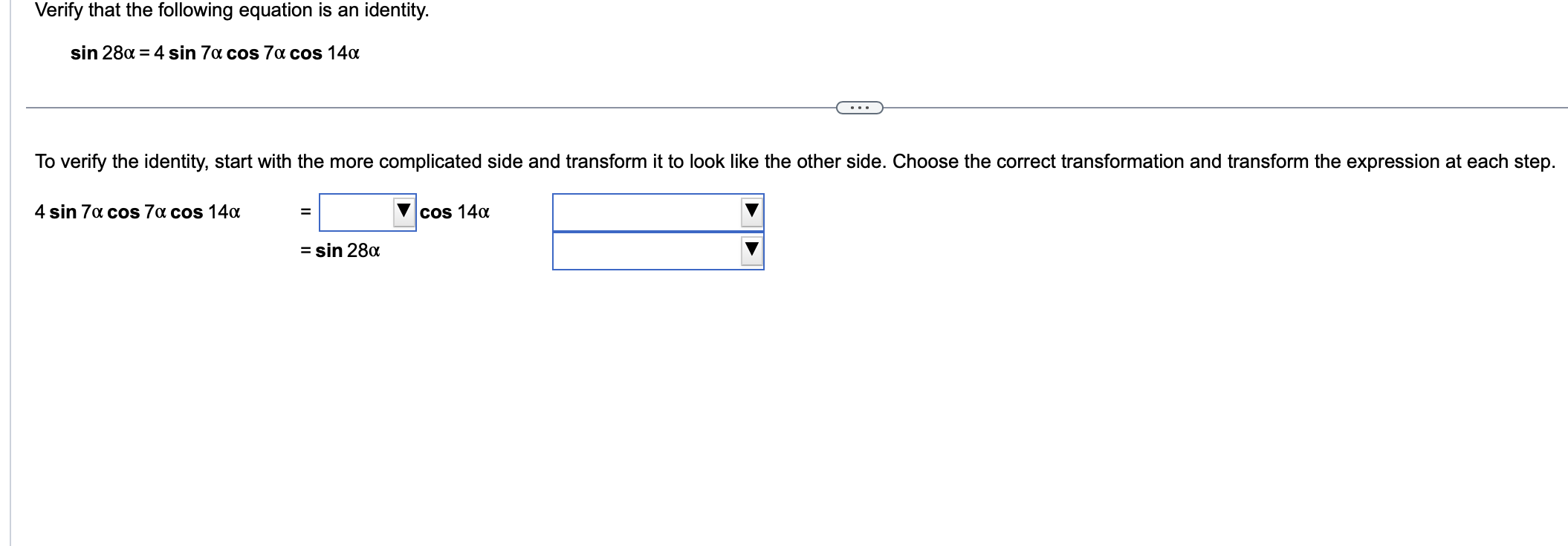
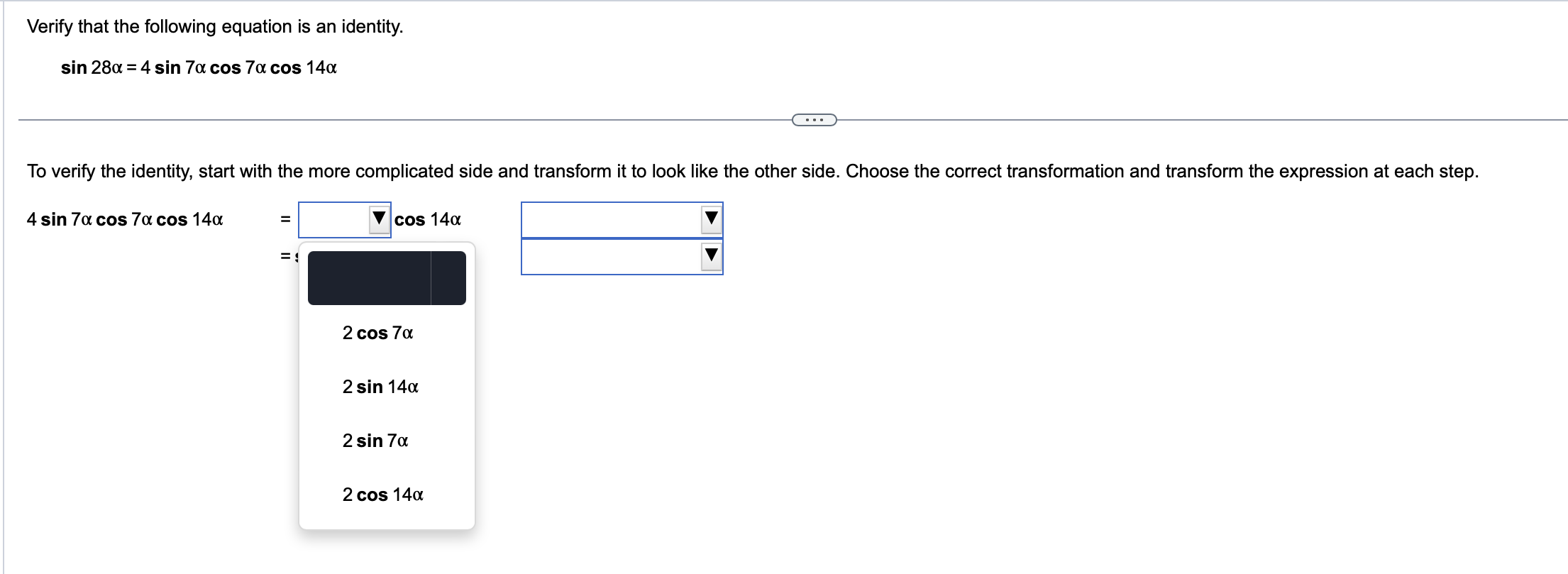
Use a sum or difference formula to find the exact value of the trigonometric function. 11x sin 12 . . . 11x sin 12 (Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.)Find the exact value of the expression by using appropriate identities. Do not use a calculator. tan 76 + tan 44 1 tan 76 tan 44 tan 76 + tan 44 D 1 tan 76 tan 44 _ Use a double-angle identity to find the exact value of the expression. cos 2 " 2 3 8 sin 00 . . . Choose the correct answer below. O A. N/ - O B. N/ - O C. V3 O D. 1/2 OE. - 13 2 OF. 1/2 2Find the expression that is equivalent to sin 60 cos 30 + cos 60 sin 30. Choose the correct answer below. {3:- sin 90 '12-} cos 90 [22'12- sin 30 '12-} cos 30 Verify the identity. (3 sin 0 - 3 cos 0)2 =9 -9 sin 20 Begin by working with the left side. Square (3 sin 0 - 3 cos 0). (Simplify your answer.) Apply a Pythagorean Identity and simplify the expression obtained in the previous step. (Simplify your answer.) The expression from the previous step then simplifies to 9 - 9 sin 20 using what? O A. Double-Angle Identity O B. Half-Angle Identity O C. Sum and Difference Identity O D. Power-Reducing IdentityVerify that the equation is an identity. cos (x + y) _1 - tan x tan y cos (x -y) 1+ tan x tany . . . Which of the following statements verifies that the equation is an identity? O A. cos (x +y) _cos xcosy - sin xsiny =1 + sinx+ cosy _1 - tan xtany cos (x - y) cos x cosy + sin xsiny cos x - sin y 1 + tan x tan y O B. 1 - tan x tan y V1 - sin (x + y) cos (x + y) cos (x + y) 1 + tan x tan y 1 - sin 2 ( x - y ) Vcos (x - y) cos (x - y) O C. sin x sin y 1 1 - tan x tan y COS X COS } cos x cosy - sin xsiny _ cos (x+y) 1 + tan x tan y sin x sin y 1+ - cos x cosy + sin xsiny cos (x-y) cos X cos yUse an identity to write the expression as a single trigonometric function value or as a single number. 1 - lsin239.1" 6 3 <:> 1 1 E-Esin239.1=|:| (Simplify your answer. Type an exact answer, using radicals as needed. Do not include the degree symbol in your answer.) Verify that the following equation is an identity. sin 280! = 4 sin 70! cos 7oz cos 14o: To verify the identity, start with the more complicated side and transform it to look like the other side. Choose the correct transformation and transform the expression at each step. 4 sin 70: cos 70: cos 140: = V cos 140: V = sin 280i V Verify that the following equation is an identity. sin 280: = 4 sin 7a cos 7a cos 14a To verify the identity, start with the more complicated side and transform it to look like the other side. Choose the correct transformation and transform the expression at each step. 4 sin 70: cos 70: cos 14m = V cos 140