Use below LINGO Model to examine lambda = 0.5, 1, 1.5, and 5.

Question: If the effect of distance decay is modified in the three-store/two-neighborhood application of Model, will this change the expected proportion of customers shopping at each store?

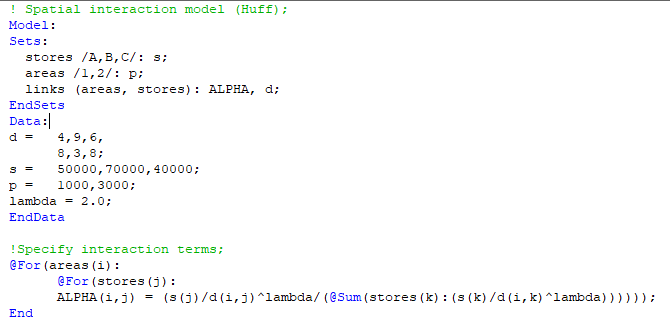
! Spatial interaction model (Huff); Model: Sets: stores /A,B,C/: 3; areas /1,2/: p; links (areas, stores): ALPHA, d; EndSets Data: d = 4,9,6, 8,3,8; S = 50000, 70000, 40000; p = 1000, 3000; lambda = 2.0; EndData ! Specify interaction terms; @For (areas (i): @For (stores (j): ALPHA(1,3) = (3 (j)/d(i,j) ^lambda/ (@Sum (stores (k): (s (k)/d(i, k) ^lambda)))))); End ! Spatial interaction model (Huff); Model: Sets: stores /A,B,C/: 3; areas /1,2/: p; links (areas, stores): ALPHA, d; EndSets Data: d = 4,9,6, 8,3,8; S = 50000, 70000, 40000; p = 1000, 3000; lambda = 2.0; EndData ! Specify interaction terms; @For (areas (i): @For (stores (j): ALPHA(1,3) = (3 (j)/d(i,j) ^lambda/ (@Sum (stores (k): (s (k)/d(i, k) ^lambda)))))); End