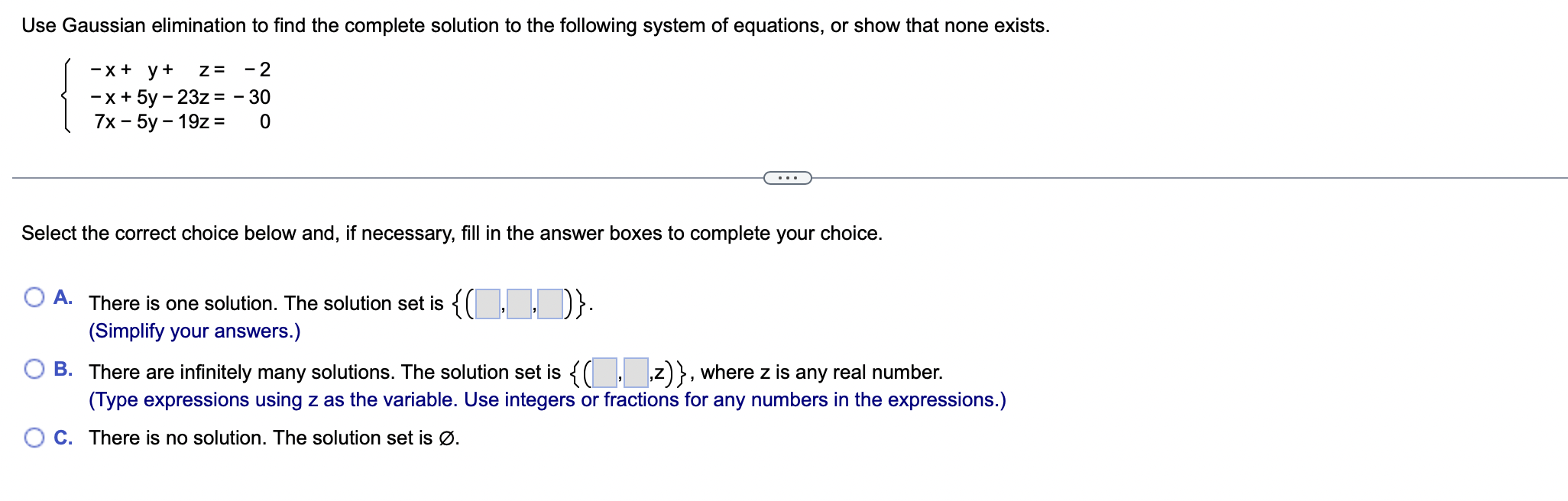
Use Gaussian elimination to find the complete solution to the following system of equations, or show that none exists. -x+ y+ z= -2 - x + 5y - 23z = -30 7x - 5y - 19z = 0 . . . Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. O A. There is one solution. The solution set is { ( , )}. (Simplify your answers.) O B. There are infinitely many solutions. The solution set is { ( , ,z) }, where z is any real number. (Type expressions using z as the variable. Use integers or fractions for any numbers in the expressions.) O C. There is no solution. The solution set is O