Use Julia programming language if needed

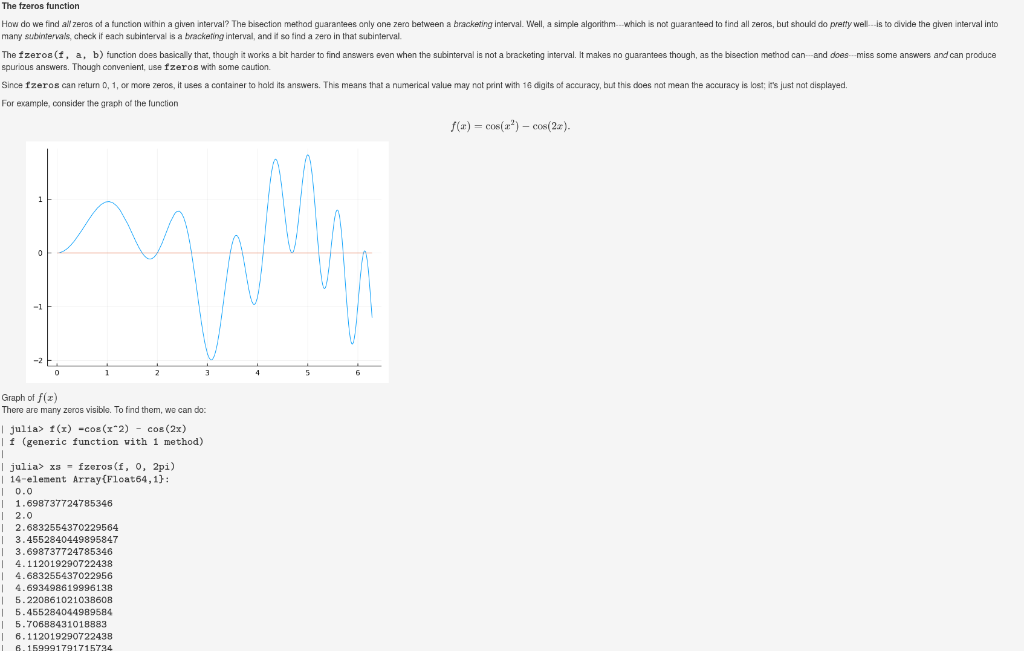
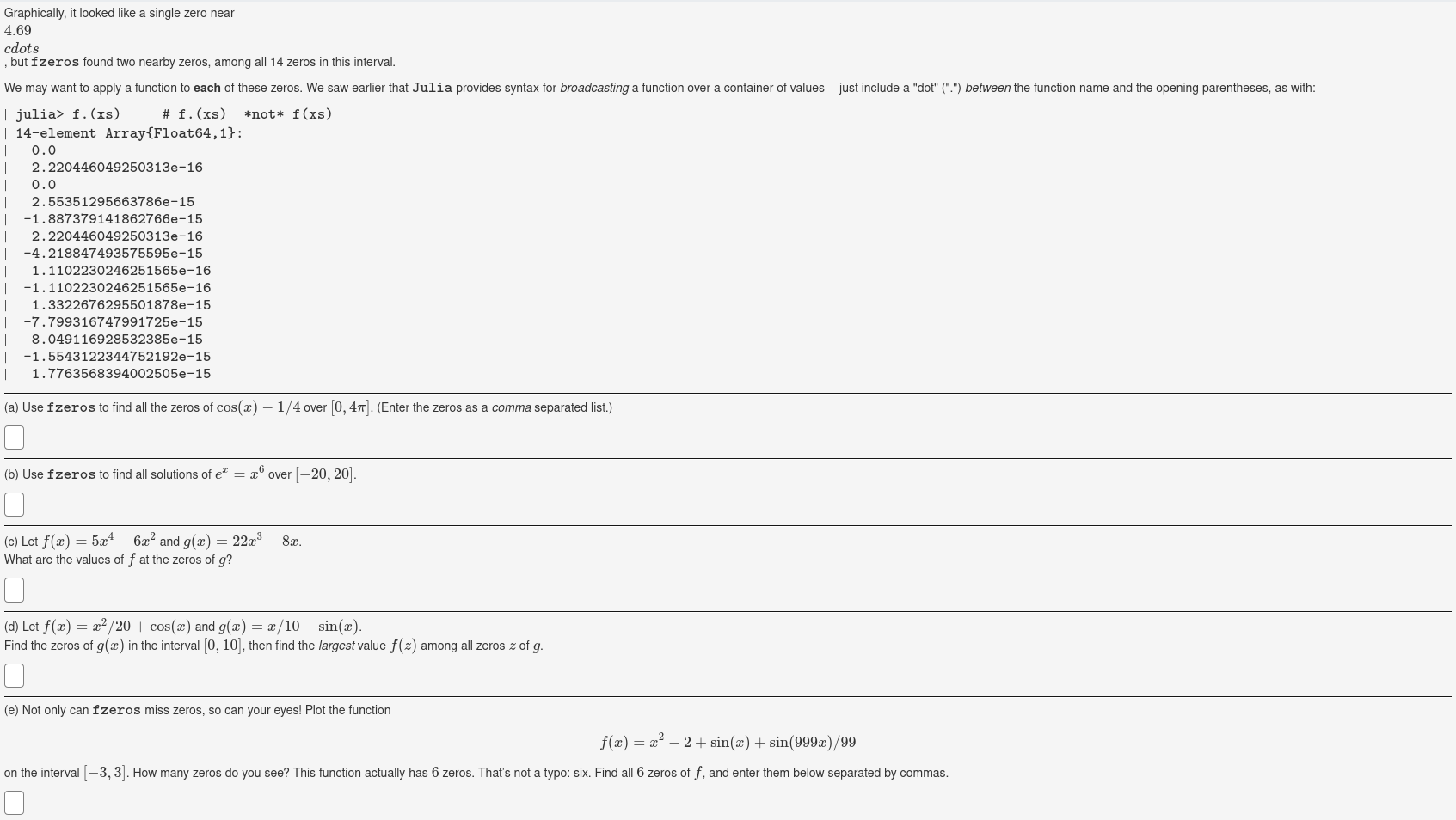
The fzeros function How do we find all zeras of a function within a given interval? The bisection method guarantees only one zera between a bracketing interval. Well, a simple algorithm --- which is not guaranteed to find all zeros, but should do pretty well--is to divide the given interval into many subintervals, check if each subinterval is a bracketing interval, and it so find a zero in that subinterval The fzeros(f, a, b) function does basically that, though it works a bit harder to find answers even when the subinterval is not a bracketing interval. It makes no guarantees though, as the bisection method can--and does-miss some answers and can produce spurious answers. Though convenient, use fzeros with some caution. Since Izeros can return 0, 1, or more zeros, it uses a container to hold its answers. This means that a numerical value y not print with 16 digits of accuracy, but this does not mean the accuracy is lost; it's just not displayed. For example, consider the graph of the function f(a) = cos(r) - cos(2x). Graph of f(x) There are many zeros visible. To find them, we can do | julia> f(1) -cos (x2) - cos (2x) | f (generic function with 1 method) | julia> x3 = fzeros(f, 0, 2pi) | 14-element Array(Float64,1): 10.0 1.698737724785346 | 2.0 12.6832554370229564 3.4552840449895847 3.698737724785346 4.112019290722438 4.683255437022956 4.693498619996138 5.22086102103860B 5.455284044989584 5.70688431018883 6.112019290722438 6. 159991791715734 Graphically, it looked like a single zero near 4.69 cdots , but fzeros found two nearby zeros, among all 14 zeros in this interval. We may want to apply a function to each of these zeros. We saw earlier that Julia provides syntax for broadcasting a function over a container of values -- just include a "dot" (".") between the function name and the opening parentheses, as with: | julia> f. (xs) # f. (xs) *not* f(xs) | 14-element Array{Float64,1}: 1 0.0 1 2.220446049250313e-16 1 0.0 | 2.55351295663786e-15 | -1.887379141862766e-15 | 2.220446049250313e-16 | -4.218847493575595e-15 1.1102230246251565e-16 -1.1102230246251565e-16 1.3322676295501878e-15 -7.799316747991725e-15 | 8.049116928532385e-15 -1.5543122344752192e-15 1.7763568394002505e-15 (a) Use fzeros to find all the zeros of cos(x) 1/4 over [0, 41]. (Enter the zeros as a comma separated list.) (b) Use fzeros to find all solutions of e" = x over (20, 20). (c) Let f(x) = 5x4 6x2 and g(x) = 22x3 87. What are the values of f at the zeros of g? (d) Let f(x) = x2/20+ cos(x) and g(x) = x/10 sin(x). Find the zeros of g(2) in the interval (0, 10), then find the largest value f(2) among all zeros z of g. (e) Not only can fzeros miss zeros, so can your eyes! Plot the function f(x) = x2 2 + sin(x) + sin(999x)/99 on the interval (-3,3]. How many zeros do you see? This function actually has 6 zeros. That's not a typo: six. Find all 6 zeros off, and enter them below separated by commas. The fzeros function How do we find all zeras of a function within a given interval? The bisection method guarantees only one zera between a bracketing interval. Well, a simple algorithm --- which is not guaranteed to find all zeros, but should do pretty well--is to divide the given interval into many subintervals, check if each subinterval is a bracketing interval, and it so find a zero in that subinterval The fzeros(f, a, b) function does basically that, though it works a bit harder to find answers even when the subinterval is not a bracketing interval. It makes no guarantees though, as the bisection method can--and does-miss some answers and can produce spurious answers. Though convenient, use fzeros with some caution. Since Izeros can return 0, 1, or more zeros, it uses a container to hold its answers. This means that a numerical value y not print with 16 digits of accuracy, but this does not mean the accuracy is lost; it's just not displayed. For example, consider the graph of the function f(a) = cos(r) - cos(2x). Graph of f(x) There are many zeros visible. To find them, we can do | julia> f(1) -cos (x2) - cos (2x) | f (generic function with 1 method) | julia> x3 = fzeros(f, 0, 2pi) | 14-element Array(Float64,1): 10.0 1.698737724785346 | 2.0 12.6832554370229564 3.4552840449895847 3.698737724785346 4.112019290722438 4.683255437022956 4.693498619996138 5.22086102103860B 5.455284044989584 5.70688431018883 6.112019290722438 6. 159991791715734 Graphically, it looked like a single zero near 4.69 cdots , but fzeros found two nearby zeros, among all 14 zeros in this interval. We may want to apply a function to each of these zeros. We saw earlier that Julia provides syntax for broadcasting a function over a container of values -- just include a "dot" (".") between the function name and the opening parentheses, as with: | julia> f. (xs) # f. (xs) *not* f(xs) | 14-element Array{Float64,1}: 1 0.0 1 2.220446049250313e-16 1 0.0 | 2.55351295663786e-15 | -1.887379141862766e-15 | 2.220446049250313e-16 | -4.218847493575595e-15 1.1102230246251565e-16 -1.1102230246251565e-16 1.3322676295501878e-15 -7.799316747991725e-15 | 8.049116928532385e-15 -1.5543122344752192e-15 1.7763568394002505e-15 (a) Use fzeros to find all the zeros of cos(x) 1/4 over [0, 41]. (Enter the zeros as a comma separated list.) (b) Use fzeros to find all solutions of e" = x over (20, 20). (c) Let f(x) = 5x4 6x2 and g(x) = 22x3 87. What are the values of f at the zeros of g? (d) Let f(x) = x2/20+ cos(x) and g(x) = x/10 sin(x). Find the zeros of g(2) in the interval (0, 10), then find the largest value f(2) among all zeros z of g. (e) Not only can fzeros miss zeros, so can your eyes! Plot the function f(x) = x2 2 + sin(x) + sin(999x)/99 on the interval (-3,3]. How many zeros do you see? This function actually has 6 zeros. That's not a typo: six. Find all 6 zeros off, and enter them below separated by commas