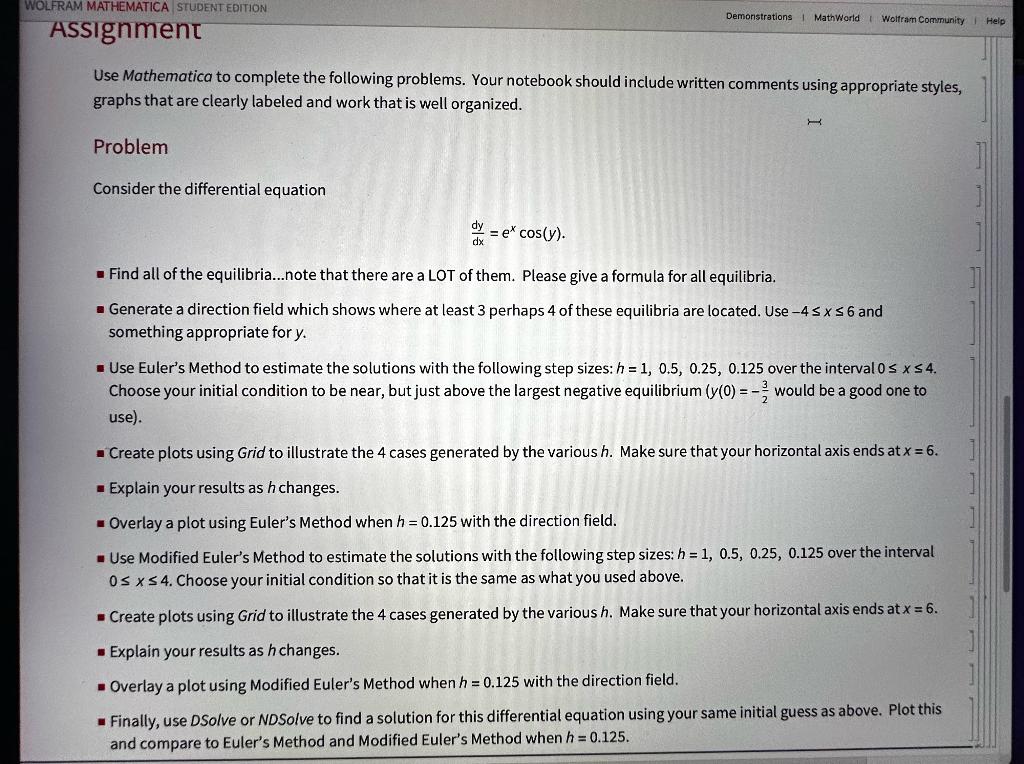
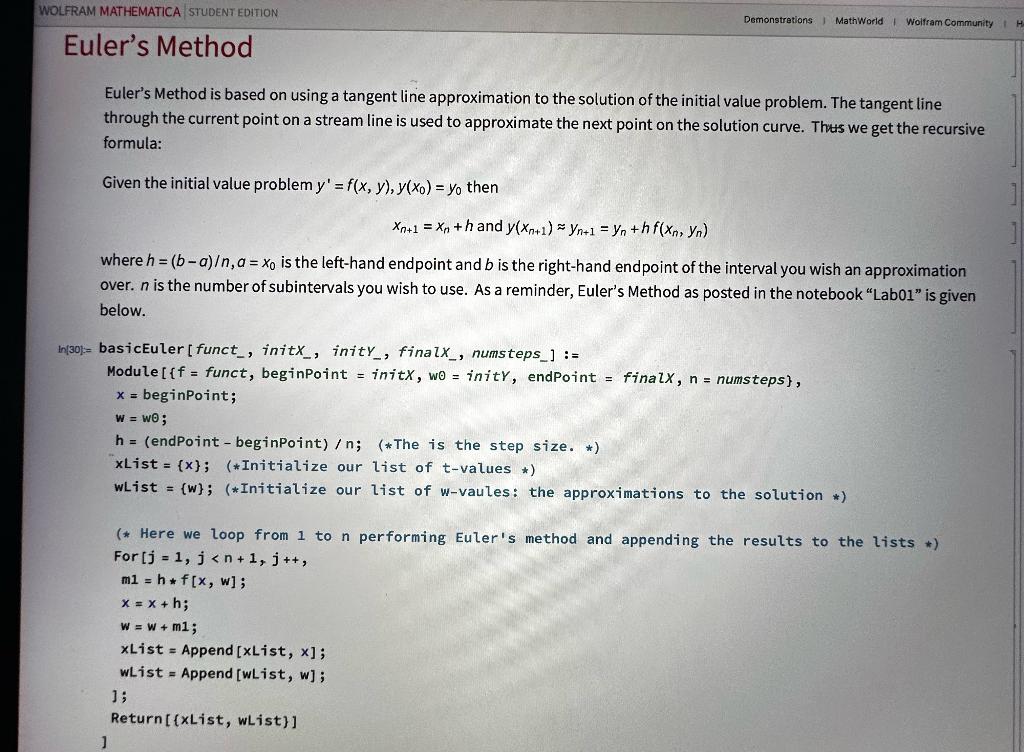
Use Mathematica to complete the following problems. Your notebook should include written comments using appropriate styles, graphs that are clearly labeled and work that is well organized. Problem Consider the differential equation dxdy=excos(y). - Find all of the equilibria...note that there are a LOT of them. Please give a formula for all equilibria. - Generate a direction field which shows where at least 3 perhaps 4 of these equilibria are located. Use 4x6 and something appropriate for y. - Use Euler's Method to estimate the solutions with the following step sizes: h=1,0.5,0.25,0.125 over the interval 0x4. Choose your initial condition to be near, but just above the largest negative equilibrium (y(0)=23 would be a good one to use). - Create plots using Grid to illustrate the 4 cases generated by the various h. Make sure that your horizontal axis ends at x=6. Explain your results as h changes. Overlay a plot using Euler's Method when h=0.125 with the direction field. Use Modified Euler's Method to estimate the solutions with the following step sizes: h=1,0.5,0.25,0.125 over the interval 0x4. Choose your initial condition so that it is the same as what you used above. - Create plots using Grid to illustrate the 4 cases generated by the various h. Make sure that your horizontal axis ends at x=6. Explain your results as h changes. - Overlay a plot using Modified Euler's Method when h=0.125 with the direction field. - Finally, use DSolve or NDSolve to find a solution for this differential equation using your same initial guess as above. Plot this and compare to Euler's Method and Modified Euler's Method when h=0.125. Euler's Method is based on using a tangent line approximation to the solution of the initial value problem. The tangent line through the current point on a stream line is used to approximate the next point on the solution curve. Thus we get the recursive formula: Given the initial value problem y=f(x,y),y(x0)=y0 then xn+1=xn+handy(xn+1)yn+1=yn+hf(xn,yn) where h=(ba),a=x0 is the left-hand endpoint and b is the right-hand endpoint of the interval you wish an approximation over. n is the number of subintervals you wish to use. As a reminder, Euler's Method as posted in the notebook "Lab01" is given below. (* Here we loop from 1 to n performing Euler's method and appending the results to the lists *) For [j=1,j