*Use Matlab

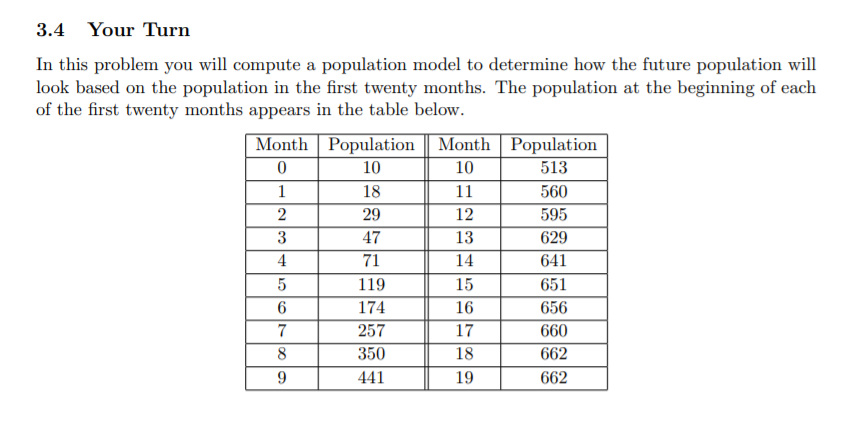
3.4 Your Turn In this problem you will compute a population model to determine how the future population will look based on the population in the first twenty months. The population at the beginning of each of the first twenty months appears in the table below. Month Population Month Population 0 10 10 513 1 18 11 560 2 29 12 595 3 47 13 629 4 71 14 641 5 119 15 651 6 174 16 656 7 257 17 660 8 350 18 662 9 441 19 662 28/55 102 Matlab Workbook 2008-2009 a) The software package loaded on your spaceship specifies the following model for the popula- tion: KPO P(t) Po + (K Poe-rt where K is the carrying capacity (maximum value) of the population, Po is the initial pop- ulation and r is the reproductive rate. Based on experimental data, you can approximate these parameters of the model using the following: Carrying Capacity: K = limt - P(t). Initial Population: Po = P(t = 0). P(2At)-(P(At) - Po) Reproductive Rate: r = t In Po(P(24t) - P(At)) Note: The computed reproductive rate r is more accurate if points that are farther apart are used for computation(i.e. points which are separated by a large At). Using these formulas, compute the parameters K, Po, and r for this model. Write down the best fit P(t) using the computed values of the parameters. Evaluate the goodness of the fit by comparing the difference between the data and the model. Plot the experimental data and the model on the same figure. In which month is the difference between the data and the model largest? How big is this difference? b) The population model given above corresponds to the logistic growth model given by P'(t)=r. P(t): (1-P) P(t) K Solve the logistic growth model using Forward Euler with a time step of 0.1, and plot it along with the previous analytical model which was specified by the software. c) Assuming that the model specified by the software in part a) is the analytical solution of the differential equation in part b), what is the Euclidean global error of your numerical logistic model obtained using Forward Euler? The expression for the Euclidean global error is given by: Global Error = (?-\yexact ynumerical 2) n ||yexact ynumerical vn where ||4|| denotes the norm of the vector v. 3.4 Your Turn In this problem you will compute a population model to determine how the future population will look based on the population in the first twenty months. The population at the beginning of each of the first twenty months appears in the table below. Month Population Month Population 0 10 10 513 1 18 11 560 2 29 12 595 3 47 13 629 4 71 14 641 5 119 15 651 6 174 16 656 7 257 17 660 8 350 18 662 9 441 19 662 28/55 102 Matlab Workbook 2008-2009 a) The software package loaded on your spaceship specifies the following model for the popula- tion: KPO P(t) Po + (K Poe-rt where K is the carrying capacity (maximum value) of the population, Po is the initial pop- ulation and r is the reproductive rate. Based on experimental data, you can approximate these parameters of the model using the following: Carrying Capacity: K = limt - P(t). Initial Population: Po = P(t = 0). P(2At)-(P(At) - Po) Reproductive Rate: r = t In Po(P(24t) - P(At)) Note: The computed reproductive rate r is more accurate if points that are farther apart are used for computation(i.e. points which are separated by a large At). Using these formulas, compute the parameters K, Po, and r for this model. Write down the best fit P(t) using the computed values of the parameters. Evaluate the goodness of the fit by comparing the difference between the data and the model. Plot the experimental data and the model on the same figure. In which month is the difference between the data and the model largest? How big is this difference? b) The population model given above corresponds to the logistic growth model given by P'(t)=r. P(t): (1-P) P(t) K Solve the logistic growth model using Forward Euler with a time step of 0.1, and plot it along with the previous analytical model which was specified by the software. c) Assuming that the model specified by the software in part a) is the analytical solution of the differential equation in part b), what is the Euclidean global error of your numerical logistic model obtained using Forward Euler? The expression for the Euclidean global error is given by: Global Error = (?-\yexact ynumerical 2) n ||yexact ynumerical vn where ||4|| denotes the norm of the vector v