USE (MATLAB APPLICATION) IN THE INSTRUCTIONS BELOW.

 

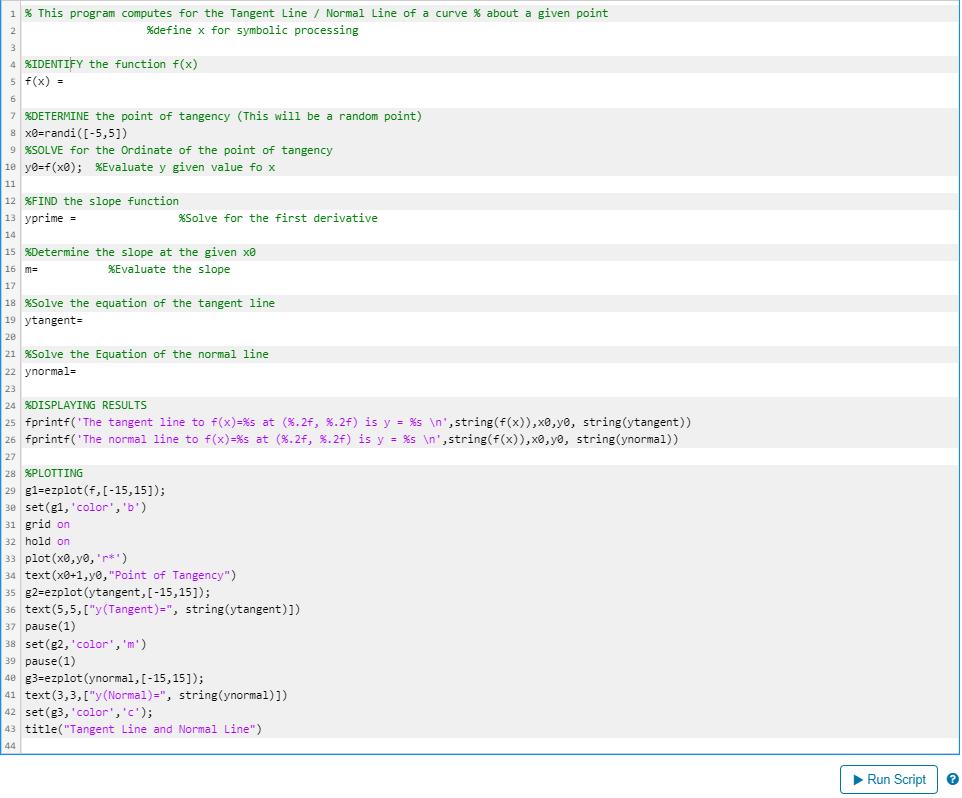
Tangent Lines and Normal Lines are included in the list of important applications of differentiation. After learning that the slope of the tangent line is the derivative of the function at the given point x=c, we can now set that m = f(c) It is is through the equation of the line, using point-slope form, we can have the equaion of the tangent line as: y-yo = m(x-xo) y = f'(xo)(x-xo) + Yo y = f'(xo)(x-xo) + f(xo) Similarly, for the normal line, since perpendicular lines have the products of the slope equals negative 1 MTL * MNL = -1 -1 MNL MTL. Thus the equation of normal line is (x-xo) + f(xo) y = f'(xo) Tangent Lines and Normal Lines are included in the list of important applications of differentiation. After learning that the slope of the tangent line is the derivative of the function at the given point x=c, we can now set that m = f(c) It is is through the equation of the line, using point-slope form, we can have the equaion of the tangent line as: y-yo = m(x-xo) y = f'(xo)(x-xo) + Yo y = f'(xo)(x-xo) + f(xo) Similarly, for the normal line, since perpendicular lines have the products of the slope equals negative 1 MTL * MNL = -1 -1 MNL MTL. Thus the equation of normal line is (x-xo) + f(xo) y = f'(xo)