USE (MATLAB APPLICATION) PLEASE BE GUIDED IN THE INSTRUCTIONS BELOW. Note: This is for double-checking purposes. I got few problem with my codes, I need guidance.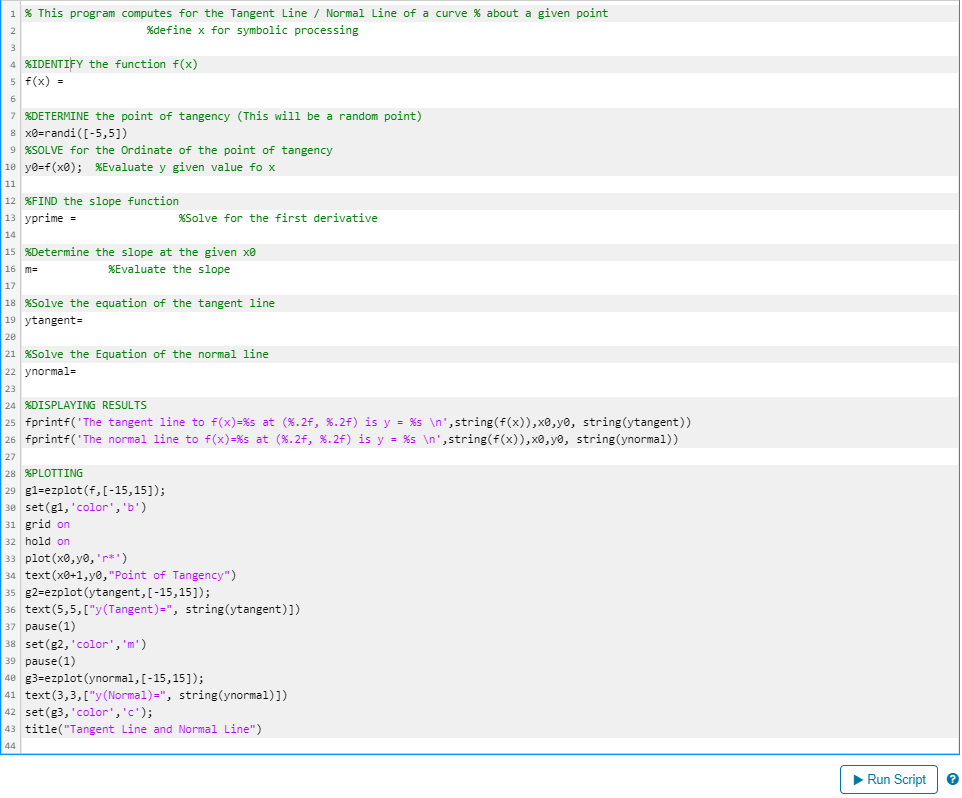

\%IDENTIFY the function f(x) f(x)= \%DETERMINE the point of tangency (This will be a random point) x=randi([5,5] ) \%SOLVE for the Ordinate of the point of tangency y=f(x); \%Evaluate y given value fo x \%FIND the slope function yprime = \%Solve for the first derivative \%Determine the slope at the given x m= \%Evaluate the slope \%Solve the equation of the tangent line ytangent= \%Solve the Equation of the normal line ynormal= \%DISPLAYING RESULTS fprintf('The tangent line to f(x)=% s at (%.2f,%.2f) is y=%s , string (f(x)),x0,y, string(ytangent)) fprintf('The normal line to f(x)=% s at (%.2f,%.2f) is y=%s , string (f(x)), x,y, string (ynormal)) \%PLOTTING g1=ezplot (f,[15,15]); set (g1,' color', 'b') grid on hold on plot(x,y,p) text (x+1,y0, "Point of Tangency") g2=ezplot (ytangent, [15,15]); text (5,5,["y( Tangent )=", string(ytangent)]) pause(1) set (g2, 'color', 'm' ) pause(1) g3=ezplot (ynormal, [15,15]); text (3,3, ["y(Normal)=", string(ynormal)]) set (g3, 'color', 'c'); title("Tangent Line and Normal Line") TANGENT LINE AND NORMAL LINES Tangent Lines and Normal Lines are included in the list of important applications of differentiation. After learning that the slope of the tangent line is the derivative of the function at the given point x=c, we can now set that - m=f(c) It is is through the equation of the line, using point-slope form, we can have the equaion of the tangent line as: - yy0=m(xx0) - y=f(x0)(xx0)+y0 - y=f(x0)(xx0)+f(x0) Similarly, for the normal line, since perpendicular lines have the products of the slope equals negative 1 - mTLmNL=1 - mNL=mTL1 Thus the equation of normal line is y=f(x0)1(xx0)+f(x0)