Use remainder theorem for alternating series to derive an approximation of pi accurate to six decimal places. For tan^-1 (1/5), I subbed 1/5 for x and 0,1,2,3, and 4 for the n values, my estimate is 0.197395663 using the remainder theorem for alternating series. For tan^-1 (1/239), my estimate was a 0.0041841. As this should be the sum of a series, my sum is very far from 3.14. I am not sure how else to approach the question.

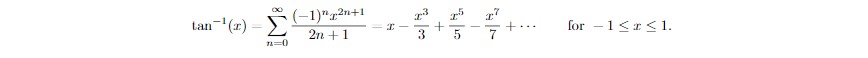
\f\f