Use the data in Solved Problem 5.1 to examine what happens to the decision if Sarah King can increase all of Design B yields from 59,000 to 64,000 by applying an expensive phosphorus to the screen at an added manufacturing cost of $250,000. Prepare the modified decision tree. What are the payoffs, and which branch has the greatest EMV?

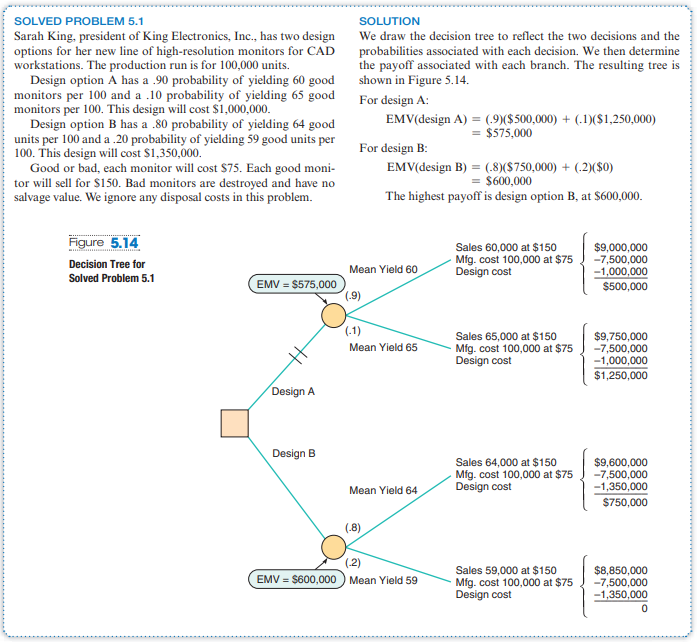
SOLVED PROBLEM 5.1 SOLUTION Sarah King, president of King Electronics, Inc., has two design We draw the decision tree to reflect the two decisions and the options for her new line of high-resolution monitors for CAD probabilities associated with each decision. We then determine workstations. The production run is for 100,000 units. the payoff associated with each branch. The resulting tree is Design option A has a 90 probability of yielding 60 good shown in Figure 5.14. monitors per 100 and a .10 probability of yielding 65 good For design A: monitors per 100 . This design will cost $1,000,000. Design option B has a .80 probability of yielding 64 good EMV( design A)=(.9)($500,000)+(.1)($1,250,000) units per 100 and a .20 probability of yielding 59 good units per 100. This design will cost $1,350,000. For design B: Good or bad, each monitor will cost $75. Each good moni- EMV ( design B) =(.8)($750,000)+(.2)($0) tor will sell for $150. Bad monitors are destroyed and have no =$600,000 salvage value. We ignore any disposal costs in this problem. The highest payoff is design option B, at $600,000