Use the fourth order Runge-Kutta method (RK4) to solve a first order initial value problem

Given the first order initial value problem:

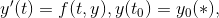with h = time step size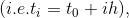

then the following formula computes an approximate solution to (*):

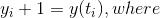
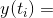true value (exact solution),

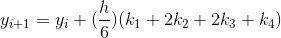and

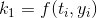
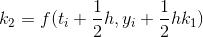
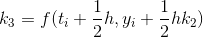
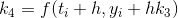
Next, consider the first order initial value problem:

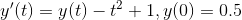
1. Solve this problem using RK4 with h = 0.5,

where from t = 0 to t = 2 with step size h = 0.5, it takes 4 steps:

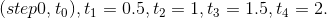
2. Complete the following table in order to compare the above results with the exact solution and errors.

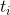	Exact Solution	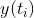Numerical solution	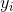Error =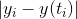
0.0	0.5	0.5	0
0.5
1.0
1.5
2.0

3. Solve and tabulate the same problem using RK4 with h=0.2.

4. Solve and tabulate the same problem using RK4 with h = 0.05.

5. Compare the errors at t = 2 for h = 0.5, h = 0.2 and h = 0.05.

Transcribed image text