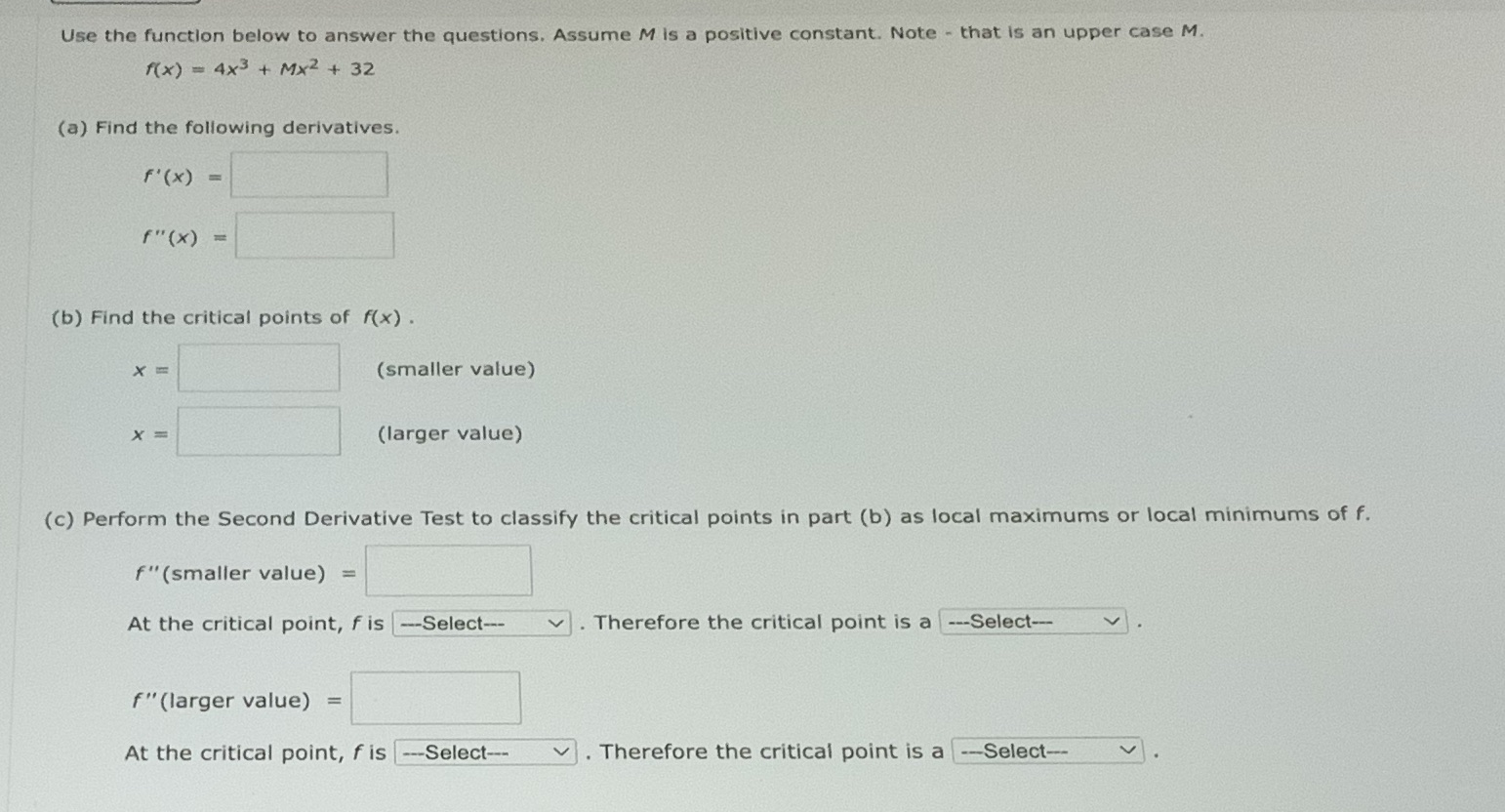
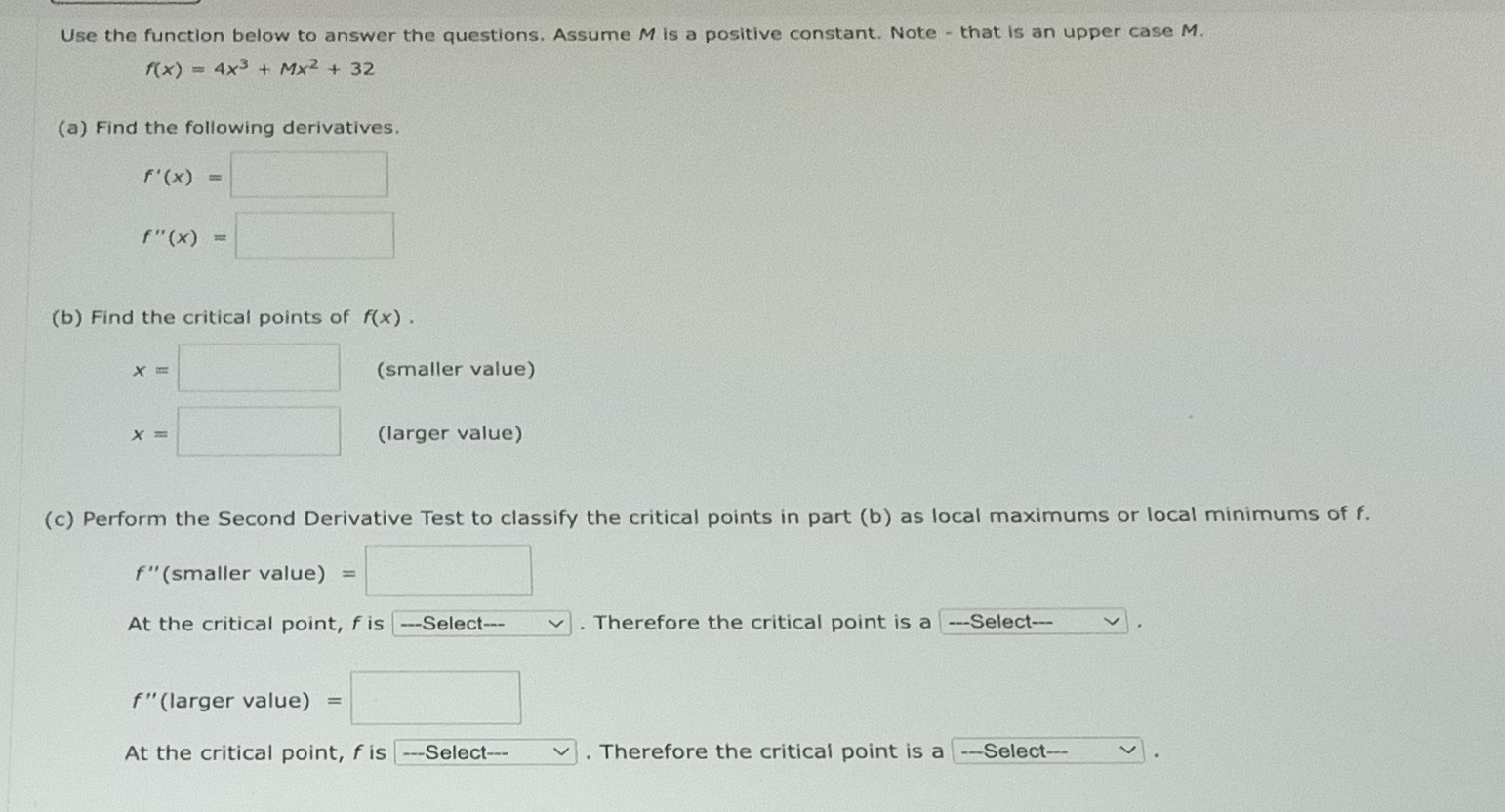
Use the function below to answer the questions. Assume M is a positive constant. Note - that is an upper case M. 1(x) = 4x3 + Mx2+ 32 (a) Find the following derivatives. f' (x ) = f" ( x ) = (b) Find the critical points of f(x) . X (smaller value) X (larger value) (c) Perform the Second Derivative Test to classify the critical points in part (b) as local maximums or local minimums of f. f" (smaller value) = At the critical point, fis --Select-- . Therefore the critical point is a ---Select-- V f"(larger value) = At the critical point, fis ---Select-- v . Therefore the critical point is a --Select