Question: Use the Master Theorem, if possible, to solve the recurrence T (n) = 3T (n/3) + 3n^3 log n. By case 1: T(n) = (n)

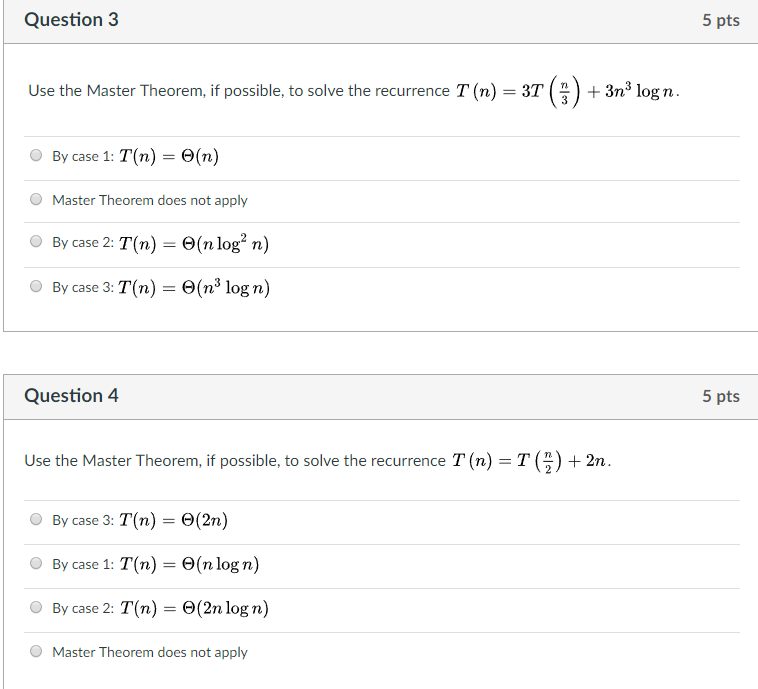
Use the Master Theorem, if possible, to solve the recurrence T

Use the Master Theorem, if possible, to solve the recurrence T (n) = 3T (n/3) + 3n^3 log n. By case 1: T(n) = (n) Master Theorem does not apply By case 2: T(n) = (n log^2 n) By case 3: T(n) = (n^3 log n) Use the Master Theorem, if possible, to solve the recurrence T (n) = T (n/2) + 2n. By case 3: T(n) = (2n) By case 1: T(n) = (n log n) By case 2: T(n) = (2 n log n) Master Theorem does not apply

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Use the Master Theorem, if possible, to solve the recurrence T (n) = 25T (n/5) + n^2. By case 2: T(n) = 0(n2 log n) Master Theorem does not apply By case 3: T(n) = (n^2) By case 1: T(n) = (n^2) Use...

Use the Master Theorem, if possible, to solve the recurrence T (n) = 4T + 4 log n. 16 By case 3: T (n) = (log n) O By case 1:T(n)-e(Vn) Master Theorem does not apply By case 2: T (n)-6(v log n)

Use the Master Theorem, if possible, to solve the recurrence T(n) = 64T (n/4) + n^2 By case 2: T(n) = Theta (n^3 log n) Master Theorem does not apply By case 1: T(n) = Theta (n^3) By case 3: T(n) =...

Use the Master Theorem, if possible, to solve the recurrence T(n) = 2T (n/2) + n/log n. By case 3: T(n) = Theta (n/log n) By case 2: T(n) = Theta (n log n) Master Theorem does not apply By case 1:...

(6 MarKs) Consider the following three methods of solving a particular problem (input size n) 1. You divide the problem into three subproblems, each ; the size of the original problem, solve each...

(6 MARKs) Consider the following three methods of solving a particular problem (input size n): 1. You divide the problem into three subproblems, each 3 the size of the original problem, solve each...

Use the master theorem to solve the following divide-and-conquer recurrence relations, and show all relevant formulations and simplifications. Indicate the case number of the master theorem for each...

Use the master theorem (if applicable) to solve the following recurrences. Show all work and state which case applies. If the master theorem does not apply, state why. a). T(n) = 7T(n/2) + n 2 log 2...

2. (60%) S is a set of points in a 2-dimensional plane. The convex hull of set S is the smallest convex set containing S. (Please find more about the convex hull problem, especially the definition of...

Input: data: array with n integers Input: n: size of data Output: permutation of data such that data[1] data[2] ...

Show that the curve r = sin tan (called a cissoid of Diocles) has the line x = 1 as a vertical asymptote. Show also that the curve lies entirely within the vertical strip 0 x

Give at least two examples of asset-backed securities.

In which situation does management integrity present the greatest amount of risk? Borrower repeatedly claims payments are made on time, when they are not. Payment history has been inconsistent...

Consider the following data for a linear reservoir which is to be waterflooded: qt = 1000 bb1/day Porosity- 18% Swi= 20% A- 50,000 square feet Water viscosity=0.62 CP Oil viscosity-2.48 cp L= 400 ft...

Holding national saving constant, does an increase in net capital outflow increase, decrease, or have no effect on a countrys accumulation of domestic capital?

An article in USA Today (December 16, 2004) began President Bush said Wednesday that the White House will shore up the sliding dollar by working to cut record budget and trade deficits. a. According...

International trade in each of the following products has increased over time. Suggest some reasons this might be so. a. wheat b. banking services c. computer software d. automobiles