Use the Master's theorem to define a Q solution to the following recurrence equation: T(n) = 2T(2n/5) + n lg n, with f(n) = n*lg(n), n > 1. To find a solution assume that the f(n) term is given by f(n) = n^a for two cases a = 1 and a = 2. Give the general Q solution for T(n) after analyzing the two polynomial cases referred to.

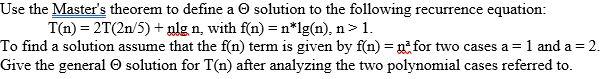
Use the Master's theorem to define a solution to the following recurrence equation: T(n) = 2T(2n/5) + nlg n, with f(n)=n*lg(n), n>1. To find a solution assume that the f(n) term is given by f(n) = n for two cases a = 1 and a = 2. Give the general solution for T(n) after analyzing the two polynomial cases referred to