Use the same problem setup as the prior exercise.

--------------------------------------------------------------------------------------------------------------

*This is the prior exercise.

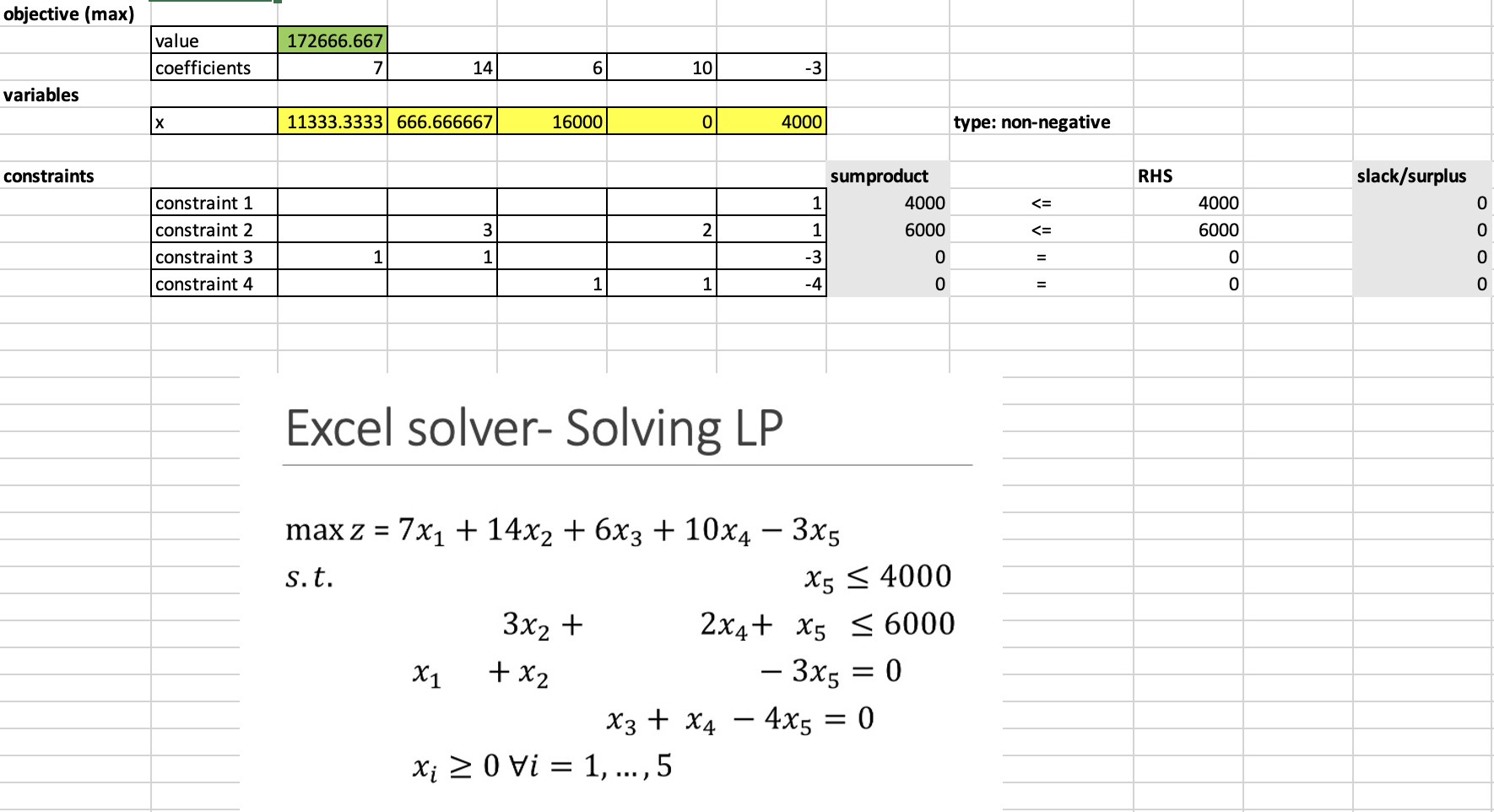
Consider a variation of the problem where R is a parameter. max z = 7x1 + 14x2 + 6x3 + 10x4 3x5 s.t. x5 4000 3x2 + 2x4 + x5 6000 x1 + x2 3x5 = R x3 + x4 4x5 = 0 xi 0 i = 1, . . . , 5 1. What are the two values a and b such that for a R b the problem is feasible? 2. How did you approach finding these bounds? 3. What is the optimal solution and objective value with R = a?

---------------------------------------------------------------------------------------------------------------

*Exercise that needs to be solved.

Consider a variation of the problem where T is a parameter. max z = 7x1 + 14x2 + 6x3 + 10x4 + T x5 s.t. x5 4000 3x2 + 2x4 + x5 6000 x1 + x2 3x5 = 0 x3 + x4 4x5 = 0 xi 0 i = 1, . . . , 5

1. For each value T = 100, 10, 100, solve the linear program. 2. Report for each value, which constraints are tight (this includes the 4 constraints of the problem + the 5 non-negativity constraints) at the optimal solution. Note: a non-negativity constraint it tight if the corresponding variable is 0 at the optimal solution.

objective (max) value coefficients 172666.667 7 14 10 -3 variables 11333.3333 666.666667 16000 0 4000 type: non-negative constraints RHS slack/surplus 0 Vi = 1, ...,5 + x2 - = =