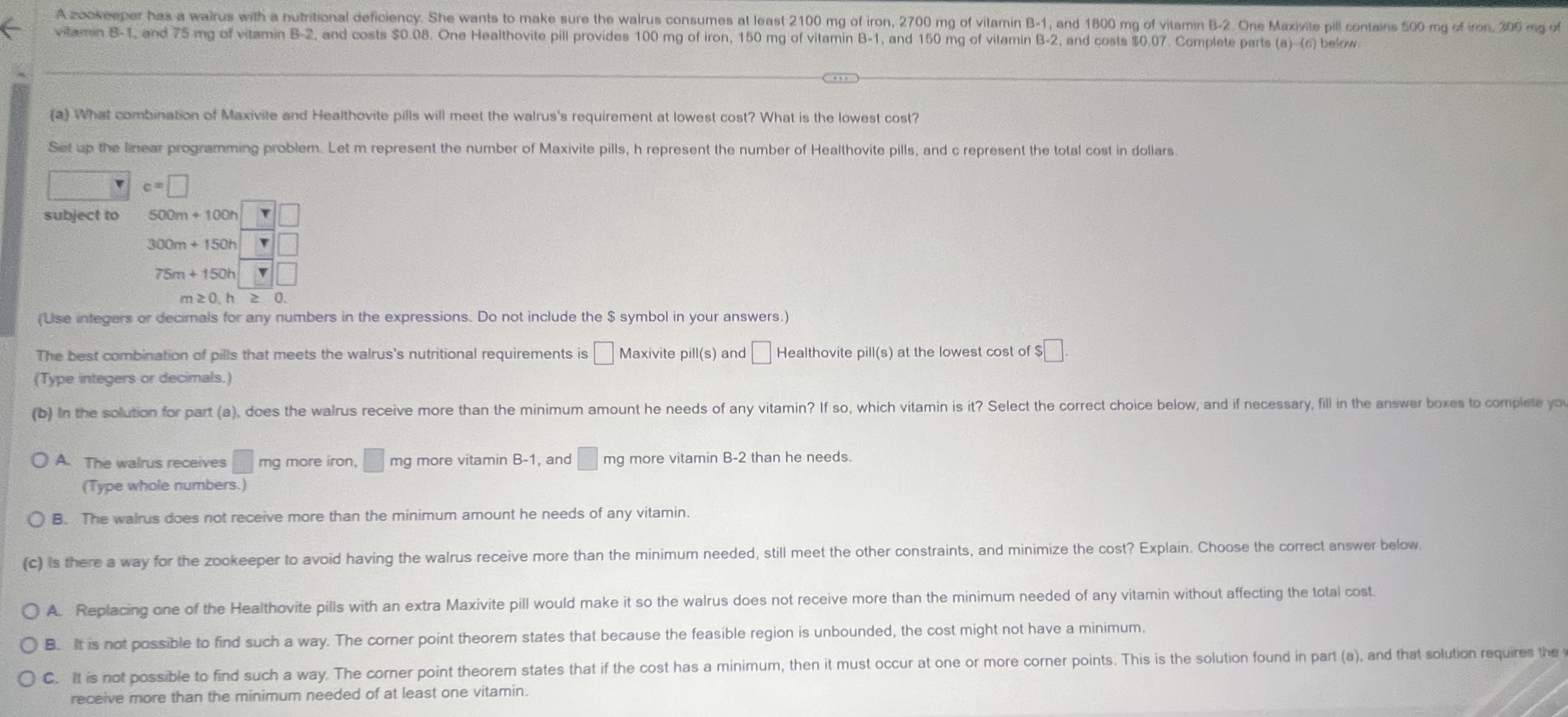
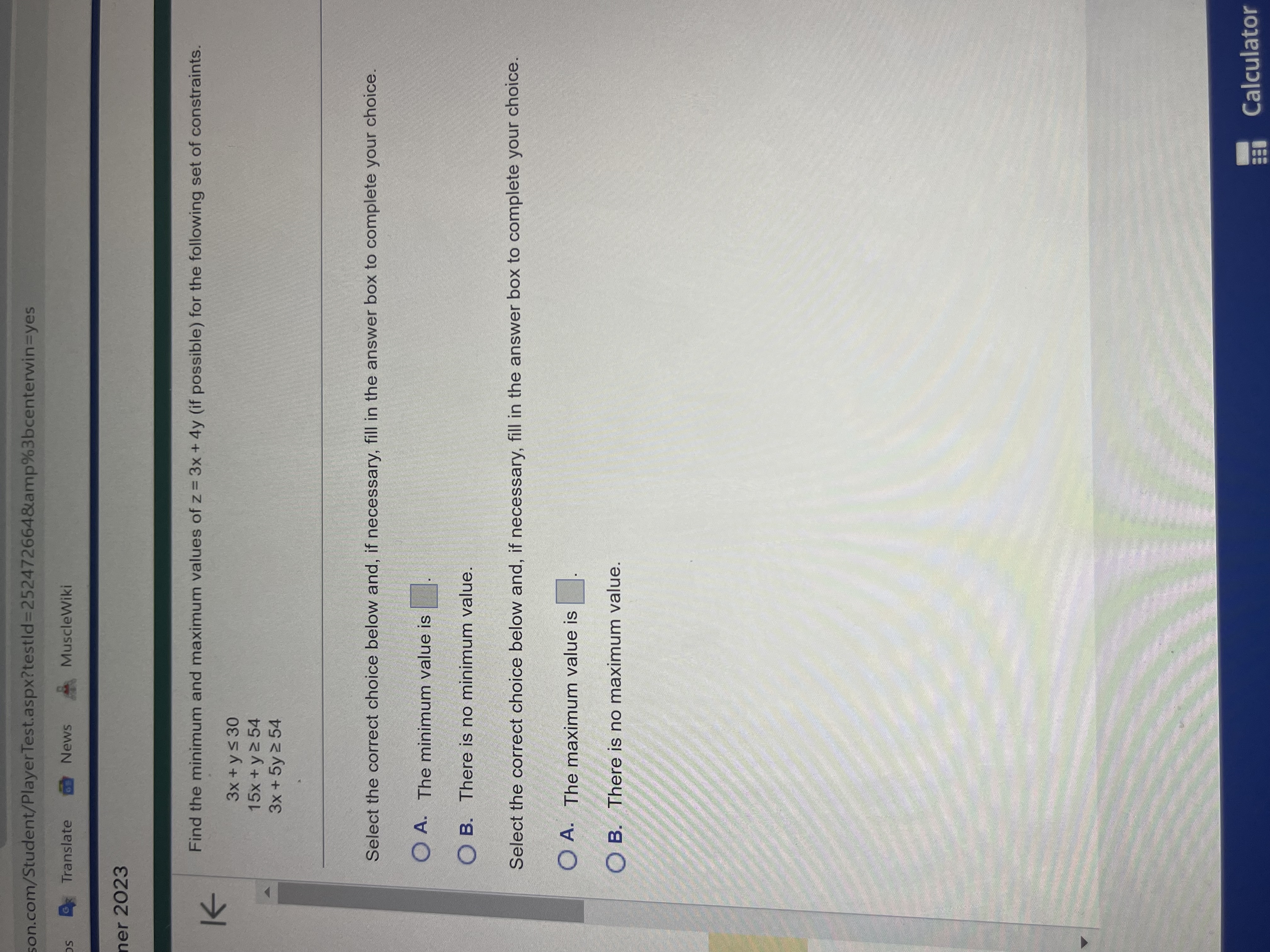
Use the simplex method to solve the linear programming problem. Maximize z = 500x, + 300x2 + 200x3 subject to X1 + X2 + X3 5 120 2x1 +3x2 +4X3 5 360 2 x1 + x2 + X3 5 160 x1 20, X2 20, X3 20. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. O A. The maximum is when x1 = , x2 = , x3 = , $1 = , $2 = , and s3 = O B. There is no maximum. W CalculatorA zookeeper has a walrus with a butritional deficiency. She wants to make sure the walrus consumes at least 2100 mg of iron, 2700 mg of vitamin B-1, and 1800 mg of vitamin B-2 One Maxivite pill contains 500 mg of iron. 200 mg of vitamin B-1, and 75 mg of vitamin B-2, and costs $0.08. One Healthovite pill provides 100 mg of iron, 150 mg of vitamin B-1, and 150 mg of vitamin B-2, and costs $0.07. Complete parts (a) (6) below (a) What combination of Maxivite and Healthovite pills will meet the walrus's requirement at lowest cost? What is the lowest cost? Set up the linear programming problem. Let m represent the number of Maxivite pills, h represent the number of Healthovite pills, and c represent the total cost in dollars subject to 500m + 100h 300m + 150h 75m + 150h m20. h 2 0. (Use integers or decimals for any numbers in the expressions. Do not include the $ symbol in your answers.) The best combination of pills that meets the walrus's nutritional requirements is Maxivite pill(s) and Healthovite pill(s) at the lowest cost of $ (Type integers or decimals.) (b) In the solution for part (a), does the walrus receive more than the minimum amount he needs of any vitamin? If so, which vitamin is it? Select the correct choice below, and if necessary, fill in the answer boxes to complete you O A The walrus receives mg more iron, mg more vitamin B-1, and mg more vitamin B-2 than he needs. (Type whole numbers.) O B. The walrus does not receive more than the minimum amount he needs of any vitamin. (c) Is there a way for the zookeeper to avoid having the walrus receive more than the minimum needed, still meet the other constraints, and minimize the cost? Explain. Choose the correct answer below. O A. Replacing one of the Healthovite pills with an extra Maxivite pill would make it so the walrus does not receive more than the minimum needed of any vitamin without affecting the total cost. O B. It is not possible to find such a way. The comer point theorem states that because the feasible region is unbounded, the cost might not have a minimum. O C. It is not possible to find such a way. The corner point theorem states that if the cost has a minimum, then it must occur at one or more corner points. This is the solution found in part (a), and that solution requires the receive more than the minimum needed of at least one vitamin.son.com/Student/PlayerTest.aspx?testld=252472664&amp%3bcenterwin=yes Translate News MuscleWiki ner 2023 K Find the minimum and maximum values of z = 3x + 4y (if possible) for the following set of constraints. 3x + ys 30 15x + y 2 54 3x + 5y 2 54 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The minimum value is O B. There is no minimum value. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The maximum value is O B. There is no maximum value. CalculatorK A manufacturer of bicycles builds 1- 3, and 10-speed models. The bicycles are made of both aluminum and steel. The company has available 43,300 units of steel and 55,300 units of aluminum. The 1-, 3-, and 10-speed models need respectively, 8, 16 and 20 units of steel and 20. 10, and 25 units of aluminum. The company makes $2 per 1-speed bike, $4 per 3-speed, and $10 per 10-speed, Use the simplex method to complete parts (a) and (b) (a) How many of each type of bicycle should be made in order to maximize profit? What is the maximum profit? Set up the linear programming problem. Let X1. X2, and x3 represent the numbers of 1-, 3-, and 10-speed bicycles, respectively, and let z be the total profit. Minimize 2 - subject to 8x, + 16%2 + 20x S 43,300 20x, + 10x2 + 25x3 S 55,300 x1 20, x2 20, X3 20 (Do not factor. Do not include the $ symbol in your answers.) The maximum profit is $ To get that profit, the company should make 1-speed bicycle(s). 3-speed bicycle(s). and 10-speed bicycle(s). (Type whole numbers.) (b) Explain what the values of the slack variables in the optimal solution mean in the context of the problem. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice QA When the profit is maximized, all of the aluminum is used but units of steel remain unused. (Type a whole number) O B. When the profit is maximized, some of each material remains unused. Specifically, units of aluminum and units of steel remain unused. (Type whole numbers.) O C. When the profit is maximized, all of the steel is used but units of aluminum remain unused (Type a whole number.) O D. When the profit is maximized, all of the available aluminum and steel is used