Use these formulas to help you solve the problems below.

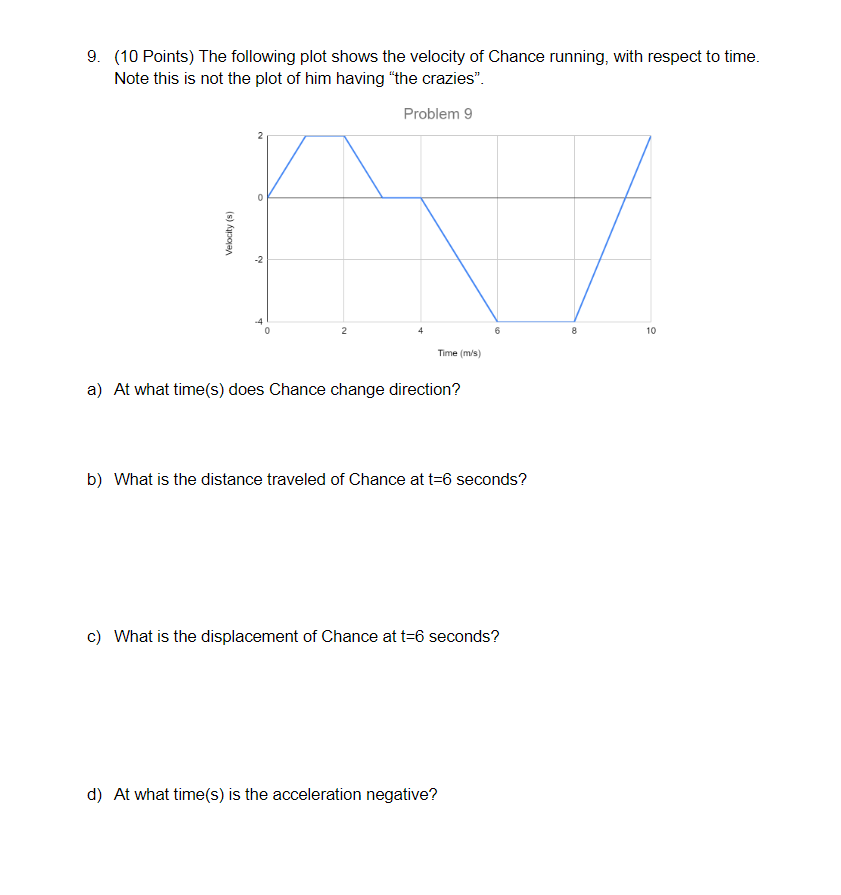
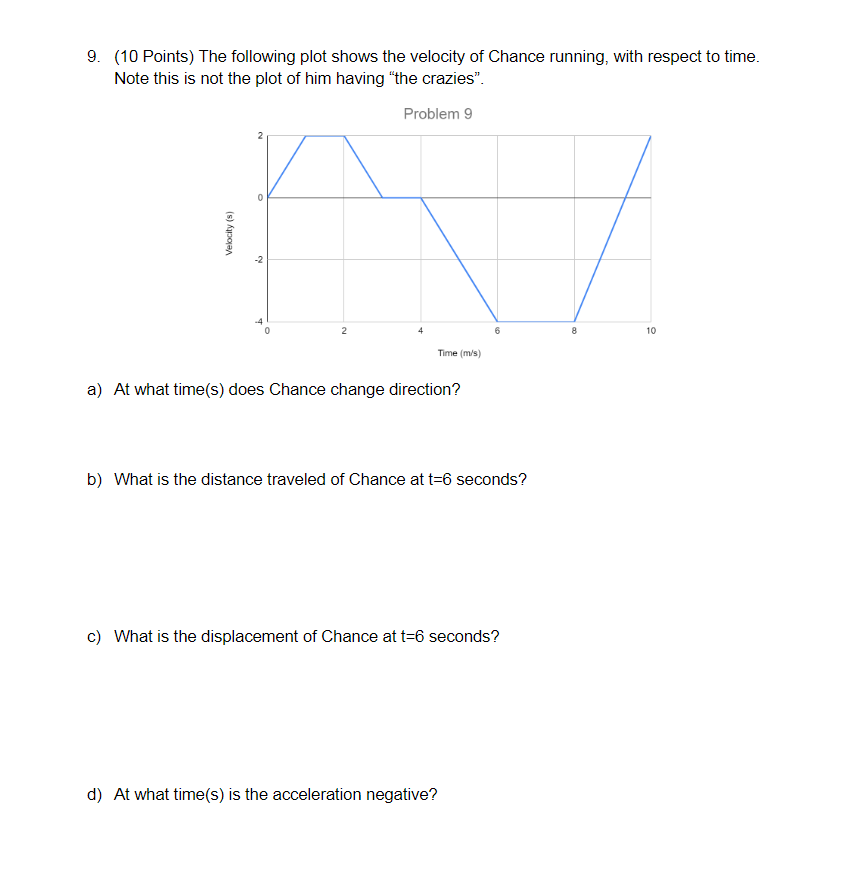
cs from Slides: Here are several still images from slides of different useful equations. 1D Motion Physics is Calculus S position V velocity a acceleration time ..... differentiate differentiate S integrate a integrate V= # S=0 V=0 a=0 particle is particle is: . momentarily at rest particle is at the origin . instantaneously at rest at constant velocity . stationary . changing directions ds : Minimum/ position set -=0, solve for f, plug back into S Maximum dv velocity set - = 0, solve for f, plug back into v yf = VitV Al+= aAtz Vyf = Vita, At 2=v z+ 2a Ay x, = X, + V At+ - a, At- 2' Vxf = Vita, At 2=V.- +2a,Ax\fWork Out: For the following questions, show all calculations for full credit. 6. (10 Points) Chance, the lovable white pitbull, has "the crazies". He is sprinting across The yard, with velocity equation Vic(t) = 4 +(0.873)] . Chance maintains this pace for 5 seconds, before making a quick turn and changing his velocity to vzc (t) = (1.5-2 )t]j .He then runs for another 6 seconds before you quit monitoring the physics of his motion and just let the dog play. a) What was the acceleration of chance, and in what direction was he accelerating, during the first 5 seconds of his run? What about the last 6 seconds? b) Over the full 11 seconds, how much distance did Chance cover? What was his displacement? c) Chance's dog friend Waffles (an objectively good dog name) is (barely) smarter than Chance and runs in a diagonal with the velocity equation "w (t) = 4|+ [5.4m]; How long does it take Waffles to reach Chance's position at 11 seconds?9. (10 Points) The following plot shows the velocity of Chance running, with respect to time. Note this is not the plot of him having "the crazies" Problem 9 Velocity (s) -2 A Time (m/'s) a) At what time(s) does Chance change direction? b) What is the distance traveled of Chance at t=6 seconds? c) What is the displacement of Chance at t=6 seconds? d) At what time(s) is the acceleration negative?Angular speed does not depend on radius linear angular position Ax do velocity V= W = dt dt dw acceleration a = Of = dt dt Galilean Transformations Position x = x'tvt x'= x- vI y = y+VI y'= y-VI E'-E-VI S velocity measured in s' velocity velocity measured in s u' = u - V u = utv velocity of s' relative to sChapter 1: This chapter was setting up the math. Familiarity with vectors is big here A . B = B . A = |AB|cos(0) | A . B = Ar Br + Ay By + AB, I AXB - -BX A = AB sin(0) | Ax B = (A,B, - A,By )it (A,Br - A.B. ) j + (A,By - AB.) k Chapter 2: Gradients are for variables that dont change with time, derivatives are for variables that change with time = TitUrAt|v. = 12 At IAc = fy vdt | a = du Uf = vi + aAt |xf = x; + viAt + zant | (of )? = (v; )2 + 2ax Chapter 3: Several topics didn't have equations, like reference frames and some directions of relative velocity. Its worth looking those parts over. Ar = (Ax)i + (Ay)y = Tri tryj | Ar = rf - ~x = ut+ x lung # 10= E dy dt AT aavg la = du At At dt | Range = " sin(20) |a. = "plac = " = w'rdisplacement Ax= X f - X; Kinematics Equations (constant acceleration) Ax = V.; + a At average velocity VE V xf At Xf = X; +VAt+-a,At2 1 total distance 2 average speed total time (v (v. )' + 2a, Ax instantaneous velocity dx V E dt Free Fall instantaneous speed Vx On Earth, when not touching anything, objects fall due to Av average acceleration a= Vf Vi gravity towards the Earth's At if - t ; center with acceleration: dv instantaneous acceleration d' x g= 9.80 m/s2 a= = dt dt2 (neglecting air resistance)