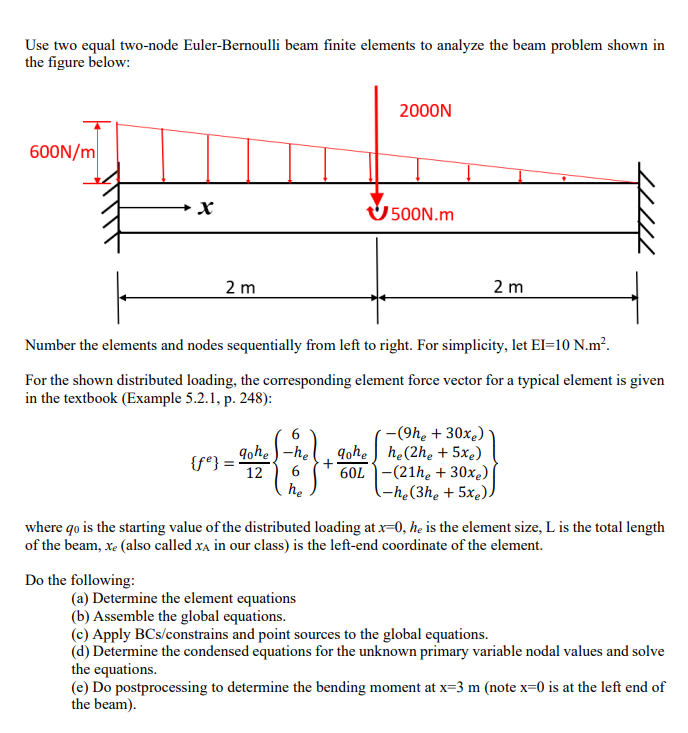
Question: Use two equal two - node Euler - Bernoulli beam finite elements to analyze the beam problem shown in the figure below: For the shown
Use two equal twonode EulerBernoulli beam finite elements to analyze the beam problem shown in the figure below:
For the shown distributed loading, the corresponding element force vector for a typical element is given in the textbook Example p:
where is the starting value of the distributed loading at is the element size, L is the total length of the beam, also called in our class is the leftend coordinate of the element.
Do the following:
a Determine the element equations
b Assemble the global equations.
c Apply BCsconstrains and point sources to the global equations.
d Determine the condensed equations for the unknown primary variable nodal values and solve the equations.
e Do postprocessing to determine the bending moment at note is at the left end of the beam
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


