Question: User Settings Course Tools Consider the beam shown in ( Figure 1 ) . ( E I ) is constant. Suppose that
User Settings
Course Tools
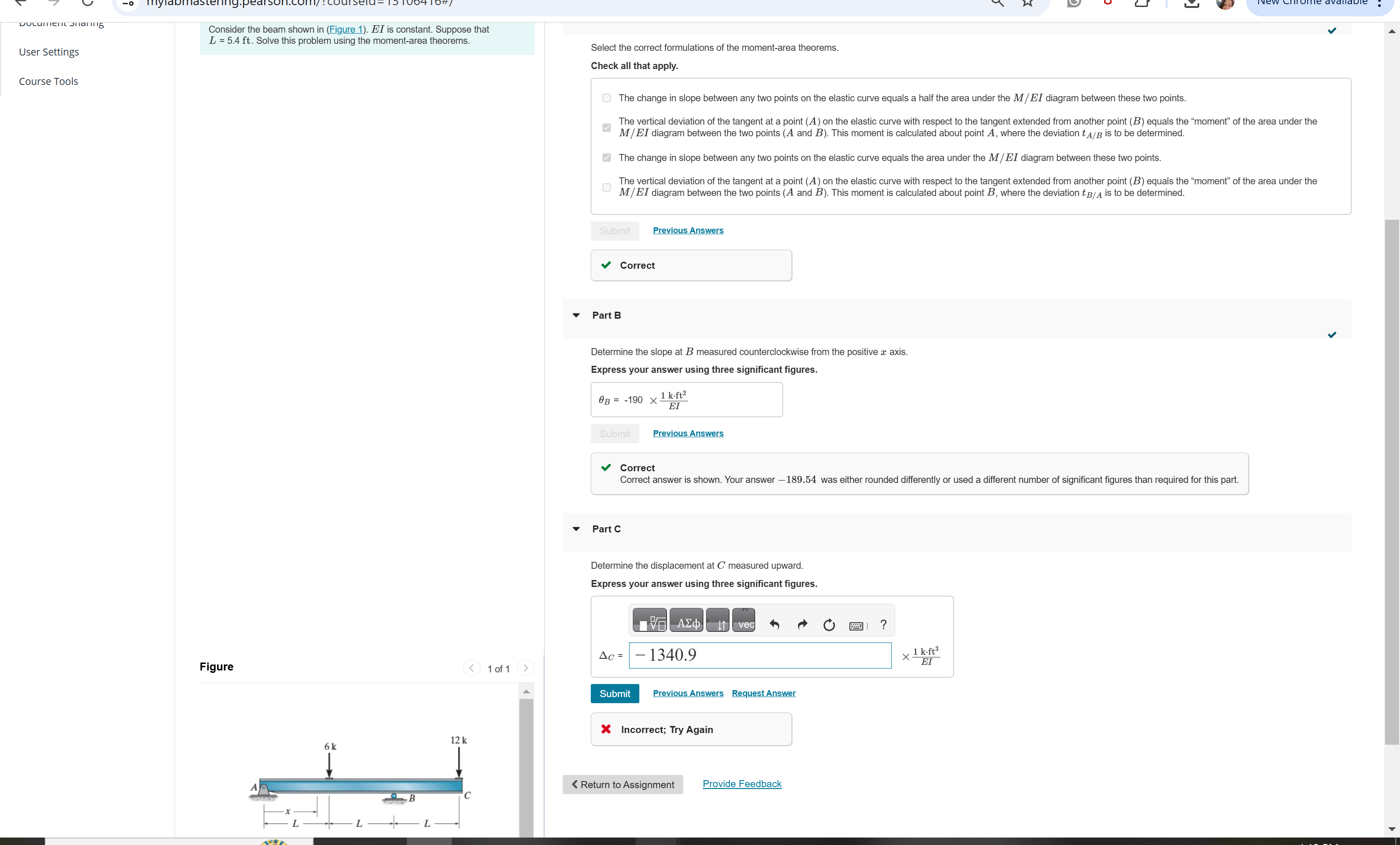
Consider the beam shown in Figure E I is constant. Suppose that
Lmathrmft Solve this problem using the momentarea theorems.
Select the correct formulations of the momentarea theorems.
Check all that apply.
The change in slope between any two points on the elastic curve equals a half the area under the M E I diagram between these two points.
The vertical deviation of the tangent at a point A on the elastic curve with respect to the tangent extended from another point B equals the "moment" of the area under the M E I diagram between the two points leftAright and B This moment is calculated about point A where the deviation tA B is to be determined.
The change in slope between any two points on the elastic curve equals the area under the M E I diagram between these two points.
The vertical deviation of the tangent at a point A on the elastic curve with respect to the tangent extended from another point B equals the "moment" of the area under the M E I diagram between the two points A and B This moment is calculated about point B where the deviation tB A is to be determined.
Correct
Part B
Determine the slope at B measured counterclockwise from the positive x axis.
Express your answer using three significant figures.
Correct
Correct answer is shown. Your answer was either rounded differently or used a different number of significant figures than required for this part.
Part C
Determine the displacement at C measured upward.
Express your answer using three significant figures.
Figure
DeltaC
times fracmathrmkcdot mathrmftE I
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


